Notations utilisées

$j$	: nombre complexe tel que $j^2=-1$
$x^*$	: conjugé
$\Re\left(u\right)$	: partie réelle de $u$
$\Im\left(u\right)$	: partie imaginaire de $u$
$\vect{x}=\left[x_1,\cdots,x_N\right]^T$	: vecteur colonne de taille $N$ et ses $N$ éléments
$\vect{x}^H$	: transposé conjugué
$\vect{x}_{a,b,c}=\left[x_a,x_b,x_c\right]^T$	: sous vecteur
$\mat{x}=\left[x_{i,j}\right]_{i=1\cdots N, j=1\cdots M}$	: matrice $N\times M$ et ses éléments
$\pstoch{x}{t}{R}$	: processus stochastique
$\va{x}$	: variable aléatoire
$\reali{x}\left(t\right)$ ou $\reali{x_{\omega}}\left(t\right)$	: $\omega^{\text{\tiny ème}}$ réalisation de ce processus stochastique
$\esp{\cdot}$	: espérance mathématique
$\esp{A\vert B}$	: espérance de $A$ conditionné par $B$
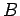$\espv{B}{A}$	: espérance calculée relativement à 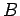$B$
$\ddp{\va{x}}\left(\omega\right)$	: densité de probabilité associée à $\va{x}$
$\frep{\va{x}}\left(\omega\right)$	: fonction de répartition associée à $\va{x}$
$\fcar{\va{x}}\left(u\right)$	: fonction caractéristique de la variable aléatoire $\va{x}$
$\sfcar{\va{x}}\left(u\right)$	: seconde fonction caractéristique de la variable aléatoire x
$\mom{\va{x}}{k}$	: moment d'ordre $k$ associé à $\va{x}$, dans le cas d'un vecteur
	de $N$ éléments, $k$ pourra être omis si $k=N$
$\cum{\va{x}}{k}$	: cumulant d'ordre $k$ associé à $\va{x}$, (même remarque concernant $k$)
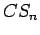$\CS{n}$	: cyclostationnaire à l'ordre $n$
$\CSP{n}$	: cyclostationnaire pur à l'ordre $n$
$\polyCS{}$	: polycyclostationnaire
$\ordre$	: ordre (l'ordre $\ordre$ correspond à $\ordre$ fois la fréquence de rotation)
$\TF{x}\left(f\right)$ ou $\TF{x}\left(\ordre\right)$	: transformée de Fourier (le contexte permettra de faire la différence
	avec la notation employée pour les variables aléatoires)
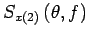$\wv{x}\left(\theta,f\right)$	: distribution de Wigner-Ville
$\swv{x}\left(\theta,f\right)$	: spectre de Wigner-Ville
$\wv{x}\left(f,\alpha\right)$	: densité de corrélation spectrale
$\speccorr{x}^{\alpha}\left(f\right)$	: densité spectrale cyclique
$\spectre{x}\left(f\right)$	: spectre
$\interspectre{x}{y}\left(f\right)$	: interspectre

$\ln\left(a\right)$	: logarithme népérien de $a$
${\log}_n \left(a\right)$	: logarithme à base $n$ de $a$
$\tilde{x}\left(t\right)$	: cepstre d'énergie de $x\left(t\right)$
$\est{x}\left(t\right)$	: estimation de $x\left(t\right)$
$a\left(t\right) \ast b\left(t\right)$	: produit de convolution de $a\left(t\right)$ par $b\left(t\right)$
$\dirac{t}$	: distribution de dirac
$\diracdec{t}{\tau}$	: distribution de dirac appliquée en $\tau$
$\diracpeigne{t}{T}$	: peigne de dirac de période $T$