| Dénomination |
Définition |
Période(s) cyclique(s) |
CS à l'ordre  |
Moment d'ordre  périodique périodique |
 |
| CS au sens large |
Cyclostationnaire à l'ordre 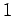 et et  |
 |
| CS au sens strict |
Fonction de répartition périodique |
 |
| CS pur |
Utilisation des cumulants au lieu des moments |
 |
| Presque-CS |
Périodicité remplacé par presque-périodicité |
 |
| |
(plusieurs cycles) |
![$K\in\left[1;\infty\right]$](img63.png) |
| PolyCS |
Le signal contient un nombre fini de cycles |
 |
| QuasiCS |
Les cycles sont incommensurables |
 |
| |
|
 |
| CS floue |
Signal cyclostationnaire observé selon une autre |
 non certain non certain |
| |
variable. |
tel que
 existe existe |
| SemiCS |
Le signal a été observé sur une durée suffisante |
|
| PseudoCS |
La durée d'observation est insuffisante. |
|
| |
Ou le signal apparait cyclostationnaire sur la |
|
| |
durée d'observation mais ne l'est pas. |
|