




Next: 5. Application de la
Up: Thèse de Frédéric BONNARDOT
Previous: 3. De la théorie
Contents
Index
Subsections
4. Cyclostationnarité floue
Jusqu'à présent, nous avons travaillé avec des signaux cyclostationnaires. Le but de ce chapitre est d'examiner le cas de signaux dont la ou les périodes cycliques ne prennent pas des valeurs certaines ; il s'agit par exemple de signaux acquis sous échantillonnage temporel, issus de machines dont la vitesse de rotation instantanée fluctue, ou bien, de signaux issus de roulements lorsque les glissements entre billes et cages font que les périodes cycliques deviennent des variables aléatoires. Afin de qualifier ce fait, nous avons introduit le vocable de ``cyclostationnarité floue''. Nous allons définir plus précisément cette notion et voir dans quelles circonstances elle peut être exploitée au même titre que la cyclostationnarité.
4.1 Définition
Une fonction
 sera dite cyclostationnaire floue (respectivement presque cyclostationnaire floue) aux ordres
sera dite cyclostationnaire floue (respectivement presque cyclostationnaire floue) aux ordres
 si et seulement s'il existe une fonction
si et seulement s'il existe une fonction
 strictement croissante, une fonction
strictement croissante, une fonction
 cyclostationnaire (respectivement presque cyclostationnaire) aux ordres
cyclostationnaire (respectivement presque cyclostationnaire) aux ordres
 , ainsi qu'un filtre variant dans le temps
, ainsi qu'un filtre variant dans le temps
 telle que l'on puisse écrire :
telle que l'on puisse écrire :
![\begin{displaymath}
h\left(t\right)=f\left[g\left(t\right)\right]\ast r\left(t,\tau\right)
\end{displaymath}](img638.png) |
(4.1) |
On prend donc en compte la relation entre l'angle et le temps d'une part en introduisant un changement de variable et d'autre part on tient compte d'un filtrage dépendant du temps et de l'angle (et donc de la vitesse de rotation), car la structure mécanique agit comme un filtre dans le domaine temporel. Dès lors, si la fluctuation de vitesse est importante, les harmoniques associées aux fréquences de rotation se déplaceront sur le spectre et n'aurons pas nécessairement la même pondération.
Dans cette partie nous allons considérer un signal vibratoire à variable générique angulaire
 (issu d'un engrenage par exemple) qui peut s'écrire :
(issu d'un engrenage par exemple) qui peut s'écrire :
 |
(4.2) |
où les  correspondent aux ordres (l'ordre
correspondent aux ordres (l'ordre  correspond à
correspond à  fois la fréquence de rotation), et les termes
fois la fréquence de rotation), et les termes
 sont des composantes stationnaires. Ce signal est cyclostationnaire à la période
sont des composantes stationnaires. Ce signal est cyclostationnaire à la période
 . Afin de l'examiner en fonction du temps
. Afin de l'examiner en fonction du temps  , nous allons utiliser une loi de position de la forme :
, nous allons utiliser une loi de position de la forme :
 |
(4.3) |
où  est la vitesse moyenne,
est la vitesse moyenne,
 caractérise les fluctuations autour de la vitesse moyenne, et,
caractérise les fluctuations autour de la vitesse moyenne, et,
 est la phase instantanée associée à
est la phase instantanée associée à
 . Nous considérons ici que les fluctuations de vitesse sont faibles vis-à-vis de la vitesse moyenne. D'autre part, nous considérons que
. Nous considérons ici que les fluctuations de vitesse sont faibles vis-à-vis de la vitesse moyenne. D'autre part, nous considérons que
 est une fonction strictement croissante, c'est-à-dire que la machine tournante associée à ce modèle ne fait pas de retour en arrière à cause de son inertie.
est une fonction strictement croissante, c'est-à-dire que la machine tournante associée à ce modèle ne fait pas de retour en arrière à cause de son inertie.
La période cyclique n'étant plus constante, on définit la période cyclique moyenne
 .
.
Si
 est cyclostationnaire, le signal
est cyclostationnaire, le signal
![$x\left(t\right)=x\left[\theta\left(t\right)\right]$](img650.png) est donc cyclostationnaire flou. Nous ne considérons pas pour l'instant l'effet du filtrage par la structure mécanique, il sera étudié séparément dans un autre paragraphe.
est donc cyclostationnaire flou. Nous ne considérons pas pour l'instant l'effet du filtrage par la structure mécanique, il sera étudié séparément dans un autre paragraphe.
Afin de caractériser la cyclostationnarité à l'ordre 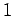 , nous allons calculer la moyenne (d'ensemble) du processus stochastique associé à
, nous allons calculer la moyenne (d'ensemble) du processus stochastique associé à
 . Soient
. Soient
 ,
,
 ,
,
 ,
,
 les processus stochastiques dont les réalisations sont respectivement
les processus stochastiques dont les réalisations sont respectivement
 ,
,
 ,
,
 et
et
 .
.
Dans le domaine temporel, nous aurons :
 |
(4.4) |
Nous devons alors calculer :
![\begin{displaymath}
\esp{C_i\left[v_{moy} t+\Phi\left(t\right)\right] e^{j\omeg...
...ht]\vert\Phi\left(t\right)} e^{j\omega_i \Phi\left(t\right)}}
\end{displaymath}](img656.png) |
(4.5) |
Où  est l'espérance de A conditionnée par B, et
est l'espérance de A conditionnée par B, et  est l'espérance calculée relativement à
est l'espérance calculée relativement à 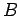 .
.
Comme
 est stationnaire,
est stationnaire,
![$C_i\left[v_{moy} t+\Phi\left(t\right)\right]$](img658.png) le sera également (l'absence de retour en arrière empêche l'apparition de périodicité). On pourra donc définir la quantité
le sera également (l'absence de retour en arrière empêche l'apparition de périodicité). On pourra donc définir la quantité  alors indépendante de
alors indépendante de
 , correspondant à :
, correspondant à :
![\begin{displaymath}
\mom{C_i}{1}=\esp{C_i\left[v_{moy} t+\Phi\left(t\right)\right]\vert\Phi\left(t\right)}
\end{displaymath}](img661.png) |
(4.6) |
Cette quantité correspond à l'amplitude de l'ordre i dans l'espérance.
Nous aurons alors :
 |
(4.7) |
Où
 est la densité de probabilité de
est la densité de probabilité de  . Finalement, l'espérance du signal dans le domaine temporel sera :
. Finalement, l'espérance du signal dans le domaine temporel sera :
![\begin{displaymath}
\esp{X\left(t\right)}=\sum_{i=1}^I \left[e^{j\omega_i v_{mo...
...omega_i \varphi} p_\phi\left(\varphi,t\right) d\varphi\right]
\end{displaymath}](img665.png) |
(4.8) |
Dans [#!antoni:cyclostationary!#], il est conclu que le moment d'ordre 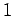 est périodique si et seulement si la fluctuation de vitesse possède des statistiques périodiques ou si elle est stationnaire. Nous allons ici, discuter plus en détail de l'interprétation de ce résultat.
est périodique si et seulement si la fluctuation de vitesse possède des statistiques périodiques ou si elle est stationnaire. Nous allons ici, discuter plus en détail de l'interprétation de ce résultat.
Supposons
 périodique à la période
périodique à la période  . Pour pouvoir trancher sur la cyclostationnarité à l'ordre
. Pour pouvoir trancher sur la cyclostationnarité à l'ordre 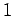 , il faut tenir compte non seulement de la période cyclique moyenne
, il faut tenir compte non seulement de la période cyclique moyenne
 mais aussi d'éventuelles périodicités dans la densité de probabilité de
mais aussi d'éventuelles périodicités dans la densité de probabilité de  .
.
Lorsque le signal est composé de plusieurs périodes cycliques, il y a deux cas possibles :
- Soit les périodes sont commensurables, alors elles ont une très forte chance d'avoir la même origine physique donc d'être soumise à la même densité de probabilité (cas des engrenages). On utilise alors leur période commune.
- Soit elles sont incommensurables et cela signifie que leurs origines physiques sont différentes, et donc que les densités de probabilité de leurs variations peuvent être très différentes également. Dans cas, il est impossible de conclure sur la cyclostationnarité.
Nous allons tout d'abord nous intéresser au terme
 . Il correspond à la transformée de Fourier de la densité de probabilité
. Il correspond à la transformée de Fourier de la densité de probabilité
 . Si cette densité est Gaussienne centrée suivant
. Si cette densité est Gaussienne centrée suivant  d'écart type
d'écart type  :
:
 |
(4.9) |
Le moment d'ordre 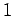 devient :
devient :
![\begin{displaymath}
\esp{X\left(t\right)}=\sum_{i=1}^I \left[e^{j\omega_i v_{mo...
...mom{C_i}{1} f\left(t\right) e^{-\omega_i^2 \sigma^2/2}\right]
\end{displaymath}](img678.png) |
(4.10) |
Cette équation comporte le terme
 , qui est d'autant plus faible que l'ordre
, qui est d'autant plus faible que l'ordre  ou que l'écart type
ou que l'écart type  sont importants. Ce terme agit donc sur le moment d'ordre
sont importants. Ce terme agit donc sur le moment d'ordre 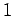 comme un filtre passe bas.
comme un filtre passe bas.
Dans le pire des cas (grande fluctuation de vitesse), l'écart type tendra vers l'infini et l'exponentielle vers 0. Le moment d'ordre 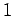 sera alors nul. Toute l'information à l'ordre
sera alors nul. Toute l'information à l'ordre 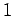 associée au cycle est donc détruite par les fluctuations de vitesse.
associée au cycle est donc détruite par les fluctuations de vitesse.
Dans le cas idéal (aucune fluctuation), l'écart type est nul, et le terme
 . Il n'y a donc plus de filtrage et toute l'information est conservée.
. Il n'y a donc plus de filtrage et toute l'information est conservée.
Ce filtrage réduit donc la quantité d'information à l'ordre 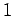 par rapport au cas cyclostationnaire.
par rapport au cas cyclostationnaire.
Pour caractériser la cyclostationnarité pure à l'ordre  , nous allons exprimer le cumulant d'ordre
, nous allons exprimer le cumulant d'ordre  [#!antoni:cyclostationary!#], nous apporterons ensuite nos propres conclusions sur le filtrage et la conservation de la cyclostationnarité :
[#!antoni:cyclostationary!#], nous apporterons ensuite nos propres conclusions sur le filtrage et la conservation de la cyclostationnarité :
Nous devons alors calculer :
![$\displaystyle \esp{C^*_m\left[v_{moy} t_1+\Phi\left(t_1\right)\right] C_n\left[...
... e^{j\left[\omega_n \Phi\left(t_2\right)-\omega_m \Phi\left(t_1\right)\right]}}$](img685.png) |
|
|
(4.14) |
![$\displaystyle = \espv{\Phi}{\esp{C^*_m\left[v_{moy} t_1+\Phi\left(t_1\right)\ri...
... e^{j\left[\omega_n \Phi\left(t_2\right)-\omega_m \Phi\left(t_1\right)\right]}}$](img686.png) |
|
|
(4.15) |
En exploitant la stationnarité de
 et donc celle de
et donc celle de
 , nous pouvons définir :
, nous pouvons définir :
![\begin{displaymath}
\mom{C_i}{2}\left[v_{moy}\left(t_2-t_1\right)+\Phi\left(t_2...
...\right)\right]\vert\Phi\left(t_1\right),\Phi\left(t_2\right)}
\end{displaymath}](img688.png) |
(4.16) |
Nous aurons alors :
Finalement, le moment d'ordre 2 du signal dans le domaine temporel sera :
![\begin{displaymath}
\cum{X\left(t\right)}{2} = \left[\sum_{m=1}^M \sum_{n=1}^N ...
...)}\right] - \esp{X^*\left(t_1\right)} \esp{X\left(t_2\right)}
\end{displaymath}](img693.png) |
(4.20) |
Cette équation est similaire à une transformée de Fourier à deux dimensions suivant  et
et  (à un signe près). Dans cette transformée de Fourier, le moment d'ordre
(à un signe près). Dans cette transformée de Fourier, le moment d'ordre  est pondéré par la densité de probabilité conjointe de
est pondéré par la densité de probabilité conjointe de
 . Comme dans le cas précédent, il est possible de faire apparaître un effet de filtrage passe bas qui conduira à une perte d'information.
. Comme dans le cas précédent, il est possible de faire apparaître un effet de filtrage passe bas qui conduira à une perte d'information.
Nous retrouvons dans l'expression du cumulant d'ordre  la densité de probabilité conjointe de la variation de vitesse, la présence de l'exponentielle
la densité de probabilité conjointe de la variation de vitesse, la présence de l'exponentielle
 et le produit des espérances de
et le produit des espérances de  . Dès lors, tout comme pour l'ordre
. Dès lors, tout comme pour l'ordre 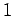 , la cyclostationnarité à l'ordre
, la cyclostationnarité à l'ordre  dépendra des propriétés des fluctuations de la période cyclique :
dépendra des propriétés des fluctuations de la période cyclique :
- Soit la période
 de
de
 est multiple ou sous multiple de la période moyenne
est multiple ou sous multiple de la période moyenne  , auquel cas le signal est cyclostationnaire selon la plus grande des périodes,
, auquel cas le signal est cyclostationnaire selon la plus grande des périodes,
- Soit les fluctuations sont stationnaires, auquel cas, la densité conjointe de probabilité ne dépend plus du temps et le signal est cyclostationnaire selon la période
 .
.
Ces calculs (mis à part les conclusions) ont été généralisés aux ordres supérieurs dans [#!raad:contributions!#].
Dans ce paragraphe, nous avons montré que sous certaines conditions, un signal cyclostationnaire flou peut devenir cyclostationnaire. Ces conditions sont assez fortes : il faut la stationnarité ou la cyclostationnarité de la variation de vitesse, avec une période cyclique multiple ou sous mutliple de la vitesse moyenne. Nous allons maintenant étudier l'effet des fluctuations de vitesse périodiques et déterministes.
Soit un signal cyclostationnaire flou associé à une fluctuation de vitesse cosinusoïdale.
Où :
 est la vitesse moyenne,
est la vitesse moyenne,
 caractérise l'amplitude de la fluctuation de vitesse,
caractérise l'amplitude de la fluctuation de vitesse,
 est la pulsation de la fluctuation de vitesse.
est la pulsation de la fluctuation de vitesse.
Le signal
 devient dans le domaine temporel :
devient dans le domaine temporel :
![\begin{displaymath}
x\left(t\right)=\sum_{i=1}^I c_i\left[\theta\left(t\right)\...
...[v_0 t+\frac{\Delta}{\alpha}\sin\left(\alpha t\right)\right]}
\end{displaymath}](img704.png) |
(4.23) |
En utilisant les fonctions de Bessel de
 espèce
espèce
 , on peut écrire :
, on peut écrire :
 |
(4.24) |
puis en remplaçant
![$c_i\left[\theta\left(t\right)\right]$](img708.png) par
par
 ,
,
 s'écrit alors :
s'écrit alors :
 |
(4.25) |
Qui aura comme transformée de Fourier :
 |
(4.26) |
Où
 est la transformée de Fourier de
est la transformée de Fourier de
 .
.
Cette équation montre que les fluctuations de vitesse vont se matérialiser par l'apparition de composantes distantes de
 par rapport au pic principal à
par rapport au pic principal à
 pondérées par des fonctions de Bessel (modulation de fréquence). La figure
pondérées par des fonctions de Bessel (modulation de fréquence). La figure ![[*]](icons/crossref.png) montre une représentation graphique des fonctions de Bessel (on obtient les termes associés aux ordres négatifs en utilisant
montre une représentation graphique des fonctions de Bessel (on obtient les termes associés aux ordres négatifs en utilisant
 pour
pour  entier).
entier).
En observant la courbe ![[*]](icons/crossref.png) du haut, on note que plus la contribution
du haut, on note que plus la contribution
 est importante, plus l'enveloppe de la courbe de Bessel est faible. Ainsi, plus l'ordre
est importante, plus l'enveloppe de la courbe de Bessel est faible. Ainsi, plus l'ordre  est grand, plus la composante
est grand, plus la composante
 est atténuée. On retrouve donc un effet de filtrage passe bas donc une perte d'information déjà mise en évidence au paragraphe précédent.
est atténuée. On retrouve donc un effet de filtrage passe bas donc une perte d'information déjà mise en évidence au paragraphe précédent.
La courbe du bas montre les pondérations
 pour un
pour un
 donné en fonction de l'ordre. Si
donné en fonction de l'ordre. Si  (pas de fluctuation), seul le coefficient
(pas de fluctuation), seul le coefficient 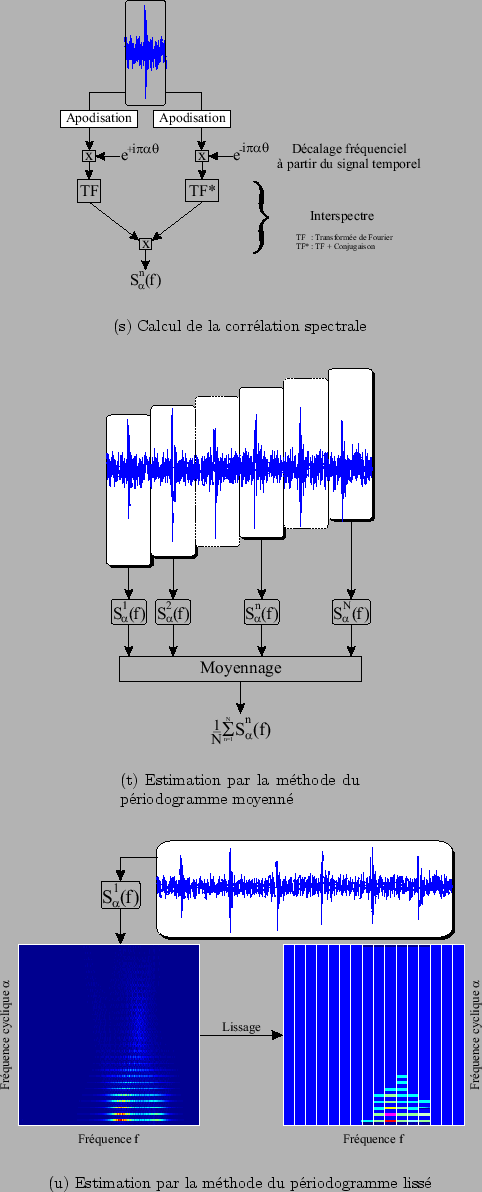 n'est pas nul. Ce résultat est logique puisqu'il supprime la pondération issue de la modulation. Lorsque la fréquence de la fluctuation de vitesse
n'est pas nul. Ce résultat est logique puisqu'il supprime la pondération issue de la modulation. Lorsque la fréquence de la fluctuation de vitesse  reste plus forte que
reste plus forte que
 , l'énergie reste concentrée autour de l'ordre
, l'énergie reste concentrée autour de l'ordre  , c'est-à-dire que l'on génère des bandes latérales de faibles amplitudes. Quand ce rapport s'inverse (par exemple à cause d'un accroissement de l'amplitude de la modulation
, c'est-à-dire que l'on génère des bandes latérales de faibles amplitudes. Quand ce rapport s'inverse (par exemple à cause d'un accroissement de l'amplitude de la modulation  ), les bandes latérales deviennent alors plus énergétiques que la composante centrale.
), les bandes latérales deviennent alors plus énergétiques que la composante centrale.
Figure:
Fonctions de Bessel de
 espèce
espèce
 |
A l'aide de cette expression nous pouvons retrouver quelques conclusions du paragraphe précédent :
Alors que dans le cas de fluctuations aléatoires, nous n'avions pas conclu lorsque les fréquences  et
et  étaient incommensurables, le cadre limitatif des fluctuations de vitesse déterministes va nous permettre de prendre en compte de telles fluctuations. En effet, bien que le processus ne soit pas nécessairement cyclostationnaire, il est toujours possible d'effectuer des moyennes synchrones. L'interprétation fréquentielle de la moyenne synchrone (filtre en peigne) nous sera particulièrement utile puisque nous connaissons la transformée de Fourier du signal. Si l'on considère que
étaient incommensurables, le cadre limitatif des fluctuations de vitesse déterministes va nous permettre de prendre en compte de telles fluctuations. En effet, bien que le processus ne soit pas nécessairement cyclostationnaire, il est toujours possible d'effectuer des moyennes synchrones. L'interprétation fréquentielle de la moyenne synchrone (filtre en peigne) nous sera particulièrement utile puisque nous connaissons la transformée de Fourier du signal. Si l'on considère que
 est relativement basse fréquence vis à vis de
est relativement basse fréquence vis à vis de  , une moyenne synchrone à la période
, une moyenne synchrone à la période
 nous permettra d'extraire la ou les composantes périodiques et d'éliminer les bandes latérales en
nous permettra d'extraire la ou les composantes périodiques et d'éliminer les bandes latérales en  . En pratique, l'efficacité de la moyenne dépendra du nombre de blocs (qui conditionne la sélectivité du filtre). Plus la valeur de
. En pratique, l'efficacité de la moyenne dépendra du nombre de blocs (qui conditionne la sélectivité du filtre). Plus la valeur de  est faible, plus le nombre de moyennes nécessaire à la disparition des modulations indésirables devra être grand.
est faible, plus le nombre de moyennes nécessaire à la disparition des modulations indésirables devra être grand.
Ainsi, lorsque la fluctuation de vitesse n'est pas à une fréquence commensurable avec
 , il est toujours possible d'utiliser la moyenne synchrone pour extraire une contribution périodique. Dans le cas contraire, les signaux conservent certes leur cyclostationnarité mais il n'est pas aussi aisé de supprimer la pollution engendrée par les fluctuations de vitesse.
, il est toujours possible d'utiliser la moyenne synchrone pour extraire une contribution périodique. Dans le cas contraire, les signaux conservent certes leur cyclostationnarité mais il n'est pas aussi aisé de supprimer la pollution engendrée par les fluctuations de vitesse.
Il est possible de généraliser ces calculs en utilisant une loi de position de la forme :
Dans ce cas, l'équation (![[*]](icons/crossref.png) ) devient :
0
) devient :
0
On obtient alors une équation plus délicate à manipuler mais permettant de prendre en compte toutes les fluctuations de vitesse périodiques. Les conclusions sont similaires au cas précédent en remplaçant  par une combinaison linéaire des
par une combinaison linéaire des  .
.
En conclusion, les fluctuations de vitesse rendront le spectre plus complexe en ajoutant de nombreuses bandes latérales. Lorsque les périodes sont incommensurables entre elles, la moyenne synchrone permet de supprimer les bandes latérales, ce qui n'est pas possible dans le cas contraire.
Nous allons rappeler les calculs faits dans [#!antoni:cyclostationary!#] et apporter nos conclusions. Avant d'arriver au capteur, les signaux vibratoires passent par la structure mécanique qui agit comme un filtre. Nous allons ici, étudier l'effet de ce filtrage. Afin d'être plus clair, nous notons la variable selon laquelle est fait le calcul à l'aide d'un indice :
 ou
ou
 .
.
Précédemment, nous avons défini la relation entre l'angle et le temps par l'équation (![[*]](icons/crossref.png) ). Etant donné qu'il n'y a pas de retour en arrière de la machine tournante, cette relation est bijective et la fonction réciproque peut s'écrire :
). Etant donné qu'il n'y a pas de retour en arrière de la machine tournante, cette relation est bijective et la fonction réciproque peut s'écrire :
 |
(4.30) |
Où
 est exprimé en
est exprimé en  , soit l'unité inverse d'une vitesse angulaire.
, soit l'unité inverse d'une vitesse angulaire.
Si
 est un processus stochastique cyclique réel, cyclostationnaire suivant
est un processus stochastique cyclique réel, cyclostationnaire suivant  de période cyclique
de période cyclique  , de réalisation
, de réalisation
 et
et
 le processus résultant du filtrage de
le processus résultant du filtrage de
 par un filtre de réponse impulsionnelle
par un filtre de réponse impulsionnelle
 , alors :
, alors :
 |
(4.31) |
Si on remplace  par
par
 , on obtient :
, on obtient :
![\begin{displaymath}
Y\left(t\right) = \int_{-\infty}^{t=u_0 \theta + \psi\left(...
...h\left[u_0 \theta + \psi\left(\theta\right)-\tau\right] d\tau
\end{displaymath}](img746.png) |
(4.32) |
Cette équation peut être écrite dans le domaine angulaire en utilisant le changement de variable
 où
où  est un retard angulaire et la notation
est un retard angulaire et la notation
![$X_\theta\left(r\right)~=~X_t\left[u_0 r+\psi\left(r\right)\right]$](img749.png) .
.
Avec :
![\begin{displaymath}
g\left(\theta,r\right)=h\left[u_0\left(\theta-r\right)+\psi...
...)-\psi\left(r\right)\right]\left[u_0+s\left(r\right)\right]
\end{displaymath}](img753.png) |
(4.35) |
Nous constatons ici que le filtre qui dépendait uniquement de  dans le domaine temporel est maintenant lié aux deux variables r et
dans le domaine temporel est maintenant lié aux deux variables r et  .
.
Les moments d'ordre  du processus à valeurs réel
du processus à valeurs réel  sont alors donnés par :
sont alors donnés par :
 |
(4.36) |
Si les fluctuations de vitesses sont déterministes, alors  le sera aussi et on pourra écrire :
le sera aussi et on pourra écrire :
 |
(4.37) |
Pour tester la cyclostationnarité de Y à la période cyclique  , posons :
, posons :
 |
(4.38) |
Le moment d'ordre  devient alors :
devient alors :
 |
(4.39) |
En exploitant la cyclostationnarité du processus  suivant l'angle, nous pouvons écrire :
suivant l'angle, nous pouvons écrire :
 |
(4.40) |
Avec :
![\begin{displaymath}
g\left(\theta+\rho,r+\rho\right)=h\left[u_0\left(\theta-r\r...
...t(r+\rho\right)\right]\left[u_0+s\left(r+\rho\right)\right]
\end{displaymath}](img759.png) |
(4.41) |
Dès lors, la cyclostationnarité du signal sera conditionnée par la périodicité du filtre g. D'après l'expression de ce filtre (équation ![[*]](icons/crossref.png) ) la périodicité de ce filtre est liée à la périodicité de
) la périodicité de ce filtre est liée à la périodicité de
 , et de sa dérivée :
, et de sa dérivée :
- si
 est périodique, à la période
est périodique, à la période  , le signal après filtrage conservera ses propriétés de cyclostationnarité à la période cyclique
, le signal après filtrage conservera ses propriétés de cyclostationnarité à la période cyclique  ,
,
- si
 est périodique, à une période
est périodique, à une période  multiple de
multiple de  , le signal ne sera plus cyclostationnaire à la période cyclique
, le signal ne sera plus cyclostationnaire à la période cyclique  mais à la période cyclique
mais à la période cyclique  ,
,
- si
 est périodique, à une période
est périodique, à une période  telle que
telle que  est multiple de
est multiple de  , alors le signal conservera ses propriétés de cyclostationnarité à la période cyclique
, alors le signal conservera ses propriétés de cyclostationnarité à la période cyclique  .
.
- dans le cas d'une fluctuation de vitesse stationnaire, le signal conservera également ses propriétés de cyclostationnarité à la période cyclique
 .
.
- dans les autres cas, le signal deviendra non stationnaire.
Pour illustrer ce cas de figure, nous allons nous appuyer sur deux modèles de signaux de roulements issus de [#!randall:relationship!#] et [#!antoni:stochastic!#]. Nous allons tout d'abord présenter le point commun de ces deux modèles, puis leurs prises en comptes différente des fluctuations de la période cyclique due au glissement entre billes et cages. Enfin, nous présenterons différents calculs issus de ses deux articles afin de montrer l'impact de ces fluctuations sur la cyclostationnarité.
4.5.1 Modèle pour les signaux accéléromètriques de roulements
La figure ![[*]](icons/crossref.png) présente les phénomènes physiques mis en jeux dans les roulements [#!mcfadden:model!#].
présente les phénomènes physiques mis en jeux dans les roulements [#!mcfadden:model!#].
Figure:
Modèle du signal vibratoire
 |
- Les chocs dus au défaut seront modélisés par une suite de diracs
 aux instants
aux instants  .
.
- Cette suite est modulée par la charge exercée entre l'arbre et le support du roulement. Un exemple de forme pour la charge est indiquée sur la figure
![[*]](icons/crossref.png) . Cette modulation sera prise en compte par une fonction
. Cette modulation sera prise en compte par une fonction
 cyclostationnaire aux ordres
cyclostationnaire aux ordres 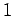 et
et  à la fréquence
à la fréquence  .
.
- Le signal
 est ensuite convolué à la réponse impulsionnelle de la structure. Comme la distance entre le défaut et le capteur n'est pas fixe, cette réponse varie au cours du temps. Elle sera représentée sous la forme d'un filtre périodique de réponse
est ensuite convolué à la réponse impulsionnelle de la structure. Comme la distance entre le défaut et le capteur n'est pas fixe, cette réponse varie au cours du temps. Elle sera représentée sous la forme d'un filtre périodique de réponse
 .
.
Dans ces conditions, il est possible d'utiliser le modèle suivant [#!antoni:stochastic!#] :
Comme le terme
 est cyclostationnaire, ses moments, périodiques, pourront s'écrire sous la forme :
est cyclostationnaire, ses moments, périodiques, pourront s'écrire sous la forme :
En raison de son caractère périodique, le filtre  peut être écrit sous la forme [#!antoni:stochastic!#] :
peut être écrit sous la forme [#!antoni:stochastic!#] :
 |
(4.46) |
où les
 représentent des filtres linéaires.
représentent des filtres linéaires.
Ce modèle est donc un cas typique de cyclostationnarité floue. En effet, on retrouve un processus cyclique
 convolué par une réponse impulsionnelle dépendant à la fois du temps et de la position des billes du roulement.
convolué par une réponse impulsionnelle dépendant à la fois du temps et de la position des billes du roulement.
Nous allons maintenant présenter deux manières de modéliser le processus générateur des instants d'impacts  .
.
Soit
 l'écart entre deux chocs. La période moyenne entre deux chocs est définie ici par
l'écart entre deux chocs. La période moyenne entre deux chocs est définie ici par
 . Le processus stochastique
. Le processus stochastique
 a été modélisé de deux manières différentes. Le premier modèle [#!randall:relationship!#], utilise une expression du type :
a été modélisé de deux manières différentes. Le premier modèle [#!randall:relationship!#], utilise une expression du type :
 |
(4.47) |
Où  représente la fluctuation de la période autour de la période moyenne. Le terme
représente la fluctuation de la période autour de la période moyenne. Le terme  sera ici modélisé par une loi normale centrée.
La figure
sera ici modélisé par une loi normale centrée.
La figure ![[*]](icons/crossref.png) (en haut) montre une réalisation simulée de
(en haut) montre une réalisation simulée de
 basée sur ce modèle (les écarts
basée sur ce modèle (les écarts  ont volontairement été exagérés). Les flèches longues indiquent la période moyenne
ont volontairement été exagérés). Les flèches longues indiquent la période moyenne  . Elles découpent le signal en blocs de taille
. Elles découpent le signal en blocs de taille  . Les petites flèches traduisent les fluctuations de vitesse
. Les petites flèches traduisent les fluctuations de vitesse  autour de la période moyenne. Cette méthode modélise une fluctuation autour d'une période moyenne. Si l'on superpose chacun des cycles (de durée
autour de la période moyenne. Cette méthode modélise une fluctuation autour d'une période moyenne. Si l'on superpose chacun des cycles (de durée  ), on obtiendra alors une distribution autour de la période moyenne dont l'écart type est celui de
), on obtiendra alors une distribution autour de la période moyenne dont l'écart type est celui de  (voir figure
(voir figure ![[*]](icons/crossref.png) ).
).
Le deuxième modèle [#!antoni:differential!#,#!antoni:stochastic!#] s'exprime par les équations suivantes :
Où  représente la fluctuation autour de l'écart moyen entre les chocs
représente la fluctuation autour de l'écart moyen entre les chocs  .
La figure
.
La figure ![[*]](icons/crossref.png) (en bas) montre une réalisation de
(en bas) montre une réalisation de
 basée sur ce modèle (les fluctuations sont les mêmes que pour la figure précédente). A la différence de la figure précédente, l'origine des flèches ne débute pas à la fin de la précédente mais après chaque choc. Il s'agit d'une marche aléatoire. Si le signal est découpé en blocs de taille
basée sur ce modèle (les fluctuations sont les mêmes que pour la figure précédente). A la différence de la figure précédente, l'origine des flèches ne débute pas à la fin de la précédente mais après chaque choc. Il s'agit d'une marche aléatoire. Si le signal est découpé en blocs de taille  et que ces derniers sont superposés, la distribution s'élargira au fil du temps. Alors que le précédent modèle traduisait un écart aléatoire par rapport à une période moyenne, celui-ci correspond à un écart aléatoire par rapport au choc précédent (figure
et que ces derniers sont superposés, la distribution s'élargira au fil du temps. Alors que le précédent modèle traduisait un écart aléatoire par rapport à une période moyenne, celui-ci correspond à un écart aléatoire par rapport au choc précédent (figure ![[*]](icons/crossref.png) ). Dès lors, le signal n'est plus synchronisé car les ``écarts s'accumulent'' : l'écart type de la distribution n'est donc plus constant mais
). Dès lors, le signal n'est plus synchronisé car les ``écarts s'accumulent'' : l'écart type de la distribution n'est donc plus constant mais  fois celui de
fois celui de  .
.
Le deuxième modèle, en contradiction avec la figure ![[*]](icons/crossref.png) est plus logique. En effet, le choc issu du défaut est lié à l'instant du dernier choc. Néanmoins, nous ne disposons pas de signaux suffisament long pour étayer cette hypothèse. Ce modèle tend à rendre le signal non stationnaire et non cyclostationnaire si l'on considère un nombre infini de périodes [#!antoni:differential!#]. Si le nombre de périodes et l'écart type sont faibles, il est possible d'utiliser le premier modèle. Il a l'avantage de générer des signaux cyclostationnaires. La figure
est plus logique. En effet, le choc issu du défaut est lié à l'instant du dernier choc. Néanmoins, nous ne disposons pas de signaux suffisament long pour étayer cette hypothèse. Ce modèle tend à rendre le signal non stationnaire et non cyclostationnaire si l'on considère un nombre infini de périodes [#!antoni:differential!#]. Si le nombre de périodes et l'écart type sont faibles, il est possible d'utiliser le premier modèle. Il a l'avantage de générer des signaux cyclostationnaires. La figure ![[*]](icons/crossref.png) montre des signaux issus de roulement possèdant un défaut sur la bague interne. On peut constater que l'approximation par le premier modèle est possible dans ce cas. L'observation d'un plus grand nombre de cycles (non disponibles) aurait peut-être conduit à une ``désynchronisation''.
montre des signaux issus de roulement possèdant un défaut sur la bague interne. On peut constater que l'approximation par le premier modèle est possible dans ce cas. L'observation d'un plus grand nombre de cycles (non disponibles) aurait peut-être conduit à une ``désynchronisation''.
Figure:
Modèles de fluctuations de vitesse
 |
Figure:
Cycles superposés
 |
Figure:
Cycles superposés - défaut de roulement sur bague interne
 |
Nous allons maintenant comparer les effets de ces deux modèles [#!randall:relationship!#] et [#!antoni:stochastic!#]. Pour cela, nous allons nous appuyer sur le formalisme décrit dans [#!srinivasan:response!#].
Nous allons dans un premier temps caractériser les impacts. Soit
 , un processus stochastique générant une série d'impacts matérialisés par des diracs :
, un processus stochastique générant une série d'impacts matérialisés par des diracs :
 |
(4.50) |
Soit
 , le nombre d'impacts rencontrés dans
, le nombre d'impacts rencontrés dans
 dans l'intervalle
dans l'intervalle
![$\left[0;T\right]$](img792.png) . Pour une réalisation donnée,
. Pour une réalisation donnée,
 apparaît comme une fonction en ``marches d'escalier''. Ces deux processus sont liés par :
apparaît comme une fonction en ``marches d'escalier''. Ces deux processus sont liés par :
 |
(4.51) |
Nous allons nous intéresser à la quantité
 qui correspond au nombre d'impacts dans l'intervalle
qui correspond au nombre d'impacts dans l'intervalle
![$\left[t,t+dt\right]$](img795.png) . En supposant que le premier impact a lieu à
. En supposant que le premier impact a lieu à  , nous pouvons écrire :
, nous pouvons écrire :
Où
 est la densité de probabilité du
est la densité de probabilité du
 impact sachant que
impact sachant que  , c'est-à-dire que
, c'est-à-dire que
 .
.
L'expression de
 dépend du modèle utilisé.
dépend du modèle utilisé.
Dans la première approche (![[*]](icons/crossref.png) ), chaque impact est situé en
), chaque impact est situé en
 . La densité de probabilité du
. La densité de probabilité du
 impact s'obtient donc en décalant celle du premier impact de
impact s'obtient donc en décalant celle du premier impact de
 , soit :
, soit :
![\begin{displaymath}
\phi_i\left(t\right)=\phi_1\left[t-\left(k-1\right) T_{moy}\right]
\end{displaymath}](img805.png) |
(4.54) |
Il est important de noter que dans cette approche,
 est indépendante du précédent tirage de
est indépendante du précédent tirage de  .
.
Dans ce cas (![[*]](icons/crossref.png) ), il est nécessaire de prendre en compte la valeur du tirage précédent de
), il est nécessaire de prendre en compte la valeur du tirage précédent de  car l'écart entre chaque impact est de
car l'écart entre chaque impact est de  . Puisque
. Puisque  , la densité de probabilité de l'impact
, la densité de probabilité de l'impact  est la densité de probabilité de
est la densité de probabilité de  . La position du
. La position du
 résulte de la somme de
résulte de la somme de  tirage de
tirage de  , dès lors, la densité de probabilité du
, dès lors, la densité de probabilité du
 impact correspondra à
impact correspondra à
 convoluée
convoluée  fois à lui-même. Soit :
fois à lui-même. Soit :
 |
(4.55) |
Quelque soit l'approche, il est également possible d'écrire
 sous la forme
sous la forme
 . Cela va nous conduire à définir la densité d'impact
. Cela va nous conduire à définir la densité d'impact
 par :
par :
 |
(4.56) |
 pourra alors être interprétée comme le nombre moyen d'impacts instantanés et
pourra alors être interprétée comme le nombre moyen d'impacts instantanés et
 comme le taux d'impact à l'instant
comme le taux d'impact à l'instant  .
.
Afin de calculer la densité d'impacts, nous allons approximer la densité de probabilité associée à
 par une loi Gaussienne de moyenne
par une loi Gaussienne de moyenne  et d'écart type
et d'écart type  :
:
 |
(4.57) |
Les figures ![[*]](icons/crossref.png) et
et ![[*]](icons/crossref.png) montrent
montrent
 pour les deux approches ainsi que son spectre pour (
pour les deux approches ainsi que son spectre pour ( et
et  ).
).
La figure du haut correspondant au ``taux d'impact moyen'' se compose d'une série de pics périodiques de période  . La transformée de Fourier sera donc :
. La transformée de Fourier sera donc :
 |
(4.58) |
La transformée de Fourier est donc une gaussienne (transformée de Fourier de
 ) multipliée par un peigne de dirac de période
) multipliée par un peigne de dirac de période  . La distribution des périodes cycliques induit ainsi un filtrage passe bas dont la fréquence de coupure sera conditionnée par son écart type. Plus l'écart type est grand, plus la fréquence de coupure est basse. Il est très important de noter que la transformée de Fourier n'est pas continue mais composée de diracs.
. La distribution des périodes cycliques induit ainsi un filtrage passe bas dont la fréquence de coupure sera conditionnée par son écart type. Plus l'écart type est grand, plus la fréquence de coupure est basse. Il est très important de noter que la transformée de Fourier n'est pas continue mais composée de diracs.
La figure du haut correspondant au ``taux d'impact moyen'' se compose d'une série de pics espacés de la période moyenne de l'impact. Au fur et à mesure que le temps passe, le pic devient de plus en plus large. En effet, comme le processus est de type marche aléatoire (
 ), la variation de la position autour de
), la variation de la position autour de  est de plus en plus importante. Lorsque le temps tend vers l'infini,
est de plus en plus importante. Lorsque le temps tend vers l'infini,  tend vers
tend vers  (chaque position devenant équiprobable, il y a un taux d'impact constant). Il est important de noter qu'ici la densité d'impacts n'est alors plus du tout périodique comme dans le cas précédent. Les signaux générés n'ont alors aucune raison d'être cyclostationnaires.
(chaque position devenant équiprobable, il y a un taux d'impact constant). Il est important de noter qu'ici la densité d'impacts n'est alors plus du tout périodique comme dans le cas précédent. Les signaux générés n'ont alors aucune raison d'être cyclostationnaires.
La transformée de Fourier est donnée par :
 |
(4.59) |
On retrouve encore une fois un effet de filtrage passe bas causé par les fluctuations de période cyclique. Il est important de noter qu'à la différence du modèle précédent, on obtient une transformée de Fourier continue (sauf à l'origine).
Figure:
Densité d'impacts
![\begin{figure}\centering
\subfigure[1$^\text{\tiny ère}$\ approche]{\epsfig{fi...
...xt{\tiny ème}$\ approche]{\epsfig{file = figures/f1s21app2.eps}}
\end{figure}](img824.png) |
Si l'écart type de
 est suffisamment faible et que l'on considère un ``faible'' nombre de cycles, le signal pourra être éventuellement approximé par un modèle cyclostationnaire. On parlera alors de pseudo-cyclostationnarité.
est suffisamment faible et que l'on considère un ``faible'' nombre de cycles, le signal pourra être éventuellement approximé par un modèle cyclostationnaire. On parlera alors de pseudo-cyclostationnarité.
La densité d'impacts et sa transformée de Fourier constituent une caractérisation à l'ordre 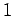 de la génération d'impacts. Pour la caractériser à l'ordre
de la génération d'impacts. Pour la caractériser à l'ordre  , nous allons utiliser la corrélation spectrale de cette densité, pour cela il nous faut d'abord calculer son autocorrélation :
, nous allons utiliser la corrélation spectrale de cette densité, pour cela il nous faut d'abord calculer son autocorrélation :
 |
(4.60) |
Il est montré dans [#!antoni:stochastic!#] que :
 |
(4.61) |
et que la transformée de Fourier de
 est donnée par :
est donnée par :
![\begin{displaymath}
F_2\left(\alpha,f\right)=F_1\left(\alpha\right)\cdot \left[F_1\left(\alpha\right)+F_1\left(\alpha-f\right)-1\right]
\end{displaymath}](img829.png) |
(4.62) |
Les figures ![[*]](icons/crossref.png) montrent les corrélations spectrales de la densité d'impact pour les
montrent les corrélations spectrales de la densité d'impact pour les  approches. Elles mettent en évidence deux points :
approches. Elles mettent en évidence deux points :
- L'effet de filtrage passe bas, du aux fluctuations de la période cyclique limite leur ``support''.
- Alors que pour la première approche, la corrélation spectrale est composée de peignes de diracs, elle apparaît continue pour la deuxième.
Figure:
Corrélation spectrale de la densité d'impact
![\begin{figure}
\subfigure[1$^\text{\tiny ère}$\ approche]{\epsfig{file = figure...
...{\tiny ère}$\ approche]{\epsfig{file = figures/cspecf1app2.eps}}
\end{figure}](img830.png) |
La relation entre  et
et  montre que
montre que  est également filtrée passe bas.
est également filtrée passe bas.
Après avoir caractérisé le processus de génération d'impacts, nous allons caractériser le signal lui même.
Rappelons l'expression du signal :
 |
(4.63) |
Les équations (![[*]](icons/crossref.png) ) et (
) et (![[*]](icons/crossref.png) ) permettent d'écrire, pour le processus stochastique
) permettent d'écrire, pour le processus stochastique
 de réalisation
de réalisation  :
:
 |
(4.64) |
Le moment d'ordre 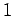 du signal est donc :
du signal est donc :
 |
(4.65) |
 est cyclostationnaire à une période
est cyclostationnaire à une période  , et
, et  est un filtre périodique à la même période.
est un filtre périodique à la même période.
Dans le cas du  modèle
modèle  est périodique à la période
est périodique à la période  , il pourra donc s'écrire sous la forme :
, il pourra donc s'écrire sous la forme :
 |
(4.66) |
En utilisant les équations (![[*]](icons/crossref.png) ) et (
) et (![[*]](icons/crossref.png) ), on obtient :
), on obtient :
![\begin{displaymath}
\esp{X\left(t\right)}=\sum_{k\in \mathbb{Z}} \sum_{m\in \ma...
...-\tau\right) e^{2\pi j\tau\left[n/T_{moy}+k f_m\right]} d\tau
\end{displaymath}](img838.png) |
(4.67) |
L'intégrale correspond à un produit de convolution avec une exponentielle, elle peut donc se mettre sous la forme.
![\begin{displaymath}
\int_0^t r_m\left(t-\tau\right) e^{2\pi j\tau\left[l/T_{moy...
..._{moy}+k f_m\right]} e^{2\pi j t\left[n/T_{moy}+k f_m\right]}
\end{displaymath}](img839.png) |
(4.68) |
Il est alors possible d'écrire l'espérance sous la forme :
 |
(4.69) |
Qui correspond à un signal quasicyclostationnaire à l'ordre 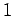 . Il sera alors possible d'extraire la partie cyclostationnaire à la période
. Il sera alors possible d'extraire la partie cyclostationnaire à la période  par moyennage synchronne.
par moyennage synchronne.
Dans le cas du
 modèle,
modèle,  n'est pas périodique, donc le signal est non cyclostationnaire. Vu la forme de
n'est pas périodique, donc le signal est non cyclostationnaire. Vu la forme de  et si
et si
 est petit, il est néanmoins possible de supposer la quasi-cyclostationnarité dans une fenêtre contenant un nombre de cycle suffisament faible (pseudo-quasi-cyclostationnarité).
est petit, il est néanmoins possible de supposer la quasi-cyclostationnarité dans une fenêtre contenant un nombre de cycle suffisament faible (pseudo-quasi-cyclostationnarité).
La fonction d'autocorrélation du signal s'écrit :
Les conclusions sont alors similaires au cas précédent : on obtient un signal quasicyclostationnaire à l'ordre  si on utilise le
si on utilise le  modèle et un signal non cyclostationnaire si l'on utilise le deuxième modèle.
modèle et un signal non cyclostationnaire si l'on utilise le deuxième modèle.
Dans ce chapitre, nous avons étudié les conditions de conservation de la cyclostationnarité quand la période cyclique fluctue. Nous avons montré qu'elle est conservée si la période cyclique moyenne est multiple ou sous multiple de la période des fluctuations.
Nous avons également mis en évidence la non cyclostationnarité des signaux de roulement, sous réserve de validité du deuxième modèle, tout en soulignant qu'il était possible de la supposer si on a affaire à un faible nombre de cycles.
L'exploitation de la cyclostationnarité dans le cas cyclostationnaire flou est moins intéressante que dans le cas cyclostationnaire car il y a un effet de filtrage passe-bas lors de l'estimation des moments et cumulants, donc une perte d'informations. C'est la raison pour laquelle il est préférable de compenser les fluctuations de vitesse en utilisant les techniques de re-échantillonnage a posteriori décrites au chapitre ![[*]](icons/crossref.png) . Dans le cas des signaux de roulement, il est évident que la suppression du ``flou'' est impossible à réaliser, cependant, le re-échantillonnage angulaire contribue à diminuer les écarts-types des distributions de périodes cycliques, donc, de diminuer les effets du filtrage passe-bas.
. Dans le cas des signaux de roulement, il est évident que la suppression du ``flou'' est impossible à réaliser, cependant, le re-échantillonnage angulaire contribue à diminuer les écarts-types des distributions de périodes cycliques, donc, de diminuer les effets du filtrage passe-bas.
L'exploitation des signaux acquis sous échantillonnage temporel reste néanmoins intéressante pour étudier les fluctuations de vitesse et en général pour tous les traitements où l'hypothèse de cyclostationnarité n'est pas nécessaire. Le domaine temporel est aussi très intéressant pour étudier les effets du filtrage des structures dont la variable générique est le temps. On pourra citer par exemple la méthode du Prony glissant [#!combet:traitement!#,#!martin:close!#] utilisant une approche non-stationnaire. Toutefois, cette technique peut être nuancée puisque les chemins de transmission évoluent suivant l'angle.
Aussi, les deux approches se révèlent alors complémentaires.





Next: 5. Application de la
Up: Thèse de Frédéric BONNARDOT
Previous: 3. De la théorie
Contents
Index
root
2005-01-05
 correspondent aux ordres (l'ordre
correspondent aux ordres (l'ordre  est la vitesse moyenne,
est la vitesse moyenne,
![\begin{displaymath}
\esp{C_i\left[v_{moy} t+\Phi\left(t\right)\right] e^{j\omeg...
...ht]\vert\Phi\left(t\right)} e^{j\omega_i \Phi\left(t\right)}}
\end{displaymath}](img656.png)
 est la densité de probabilité de
est la densité de probabilité de  périodique à la période
périodique à la période ![\begin{displaymath}
\esp{X\left(t\right)}=\sum_{i=1}^I \left[e^{j\omega_i v_{mo...
...mom{C_i}{1} f\left(t\right) e^{-\omega_i^2 \sigma^2/2}\right]
\end{displaymath}](img678.png)
 , qui est d'autant plus faible que l'ordre
, qui est d'autant plus faible que l'ordre 
![$\displaystyle \esp{C^*_m\left[v_{moy} t_1+\Phi\left(t_1\right)\right] C_n\left[...
... e^{j\left[\omega_n \Phi\left(t_2\right)-\omega_m \Phi\left(t_1\right)\right]}}$](img685.png)
![$\displaystyle \quad \quad \cdots e^{j\left[\omega_n \varphi_2-\omega_m \varphi_1\right]} d\varphi_1 d\varphi_2$](img692.png)
 et
et  est la vitesse moyenne,
est la vitesse moyenne,
 espèce
espèce
![$c_i\left[\theta\left(t\right)\right]$](img708.png) par
par

 est la transformée de Fourier de
est la transformée de Fourier de
 n'est pas nul. Ce résultat est logique puisqu'il supprime la pondération issue de la modulation. Lorsque la fréquence de la fluctuation de vitesse
n'est pas nul. Ce résultat est logique puisqu'il supprime la pondération issue de la modulation. Lorsque la fréquence de la fluctuation de vitesse  , alors, pour chacune des valeurs de
, alors, pour chacune des valeurs de 
![$\displaystyle \sum_{i=1}^I \sum_{n_1=-\infty}^{+\infty} \cdots \sum_{n_K=-\inft...
...ight] D_i\left(f-\frac{\omega_i v_0+\sum_{k=1}^K n_k \alpha_{s_k}}{2\pi}\right)$](img734.png)
 par une combinaison linéaire des
par une combinaison linéaire des  est exprimé en
est exprimé en  , on obtient :
, on obtient :
 où
où 
![\begin{displaymath}
g\left(\theta,r\right)=h\left[u_0\left(\theta-r\right)+\psi...
...)-\psi\left(r\right)\right]\left[u_0+s\left(r\right)\right]
\end{displaymath}](img753.png)
 sont alors donnés par :
sont alors donnés par :



![\begin{displaymath}
g\left(\theta+\rho,r+\rho\right)=h\left[u_0\left(\theta-r\r...
...t(r+\rho\right)\right]\left[u_0+s\left(r+\rho\right)\right]
\end{displaymath}](img759.png)
 , et de sa dérivée :
, et de sa dérivée :
 aux instants
aux instants 


 représentent des filtres linéaires.
représentent des filtres linéaires.
 représente la fluctuation de la période autour de la période moyenne. Le terme
représente la fluctuation de la période autour de la période moyenne. Le terme  fois celui de
fois celui de 


 , le nombre d'impacts rencontrés dans
, le nombre d'impacts rencontrés dans
 qui correspond au nombre d'impacts dans l'intervalle
qui correspond au nombre d'impacts dans l'intervalle

 est la densité de probabilité du
est la densité de probabilité du
 . Cela va nous conduire à définir la densité d'impact
. Cela va nous conduire à définir la densité d'impact
 et
et  . La distribution des périodes cycliques induit ainsi un filtrage passe bas dont la fréquence de coupure sera conditionnée par son écart type. Plus l'écart type est grand, plus la fréquence de coupure est basse. Il est très important de noter que la transformée de Fourier n'est pas continue mais composée de diracs.
. La distribution des périodes cycliques induit ainsi un filtrage passe bas dont la fréquence de coupure sera conditionnée par son écart type. Plus l'écart type est grand, plus la fréquence de coupure est basse. Il est très important de noter que la transformée de Fourier n'est pas continue mais composée de diracs.
![\begin{figure}\centering
\subfigure[1$^\text{\tiny ère}$\ approche]{\epsfig{fi...
...xt{\tiny ème}$\ approche]{\epsfig{file = figures/f1s21app2.eps}}
\end{figure}](img824.png)
 est suffisamment faible et que l'on considère un ``faible'' nombre de cycles, le signal pourra être éventuellement approximé par un modèle cyclostationnaire. On parlera alors de pseudo-cyclostationnarité.
est suffisamment faible et que l'on considère un ``faible'' nombre de cycles, le signal pourra être éventuellement approximé par un modèle cyclostationnaire. On parlera alors de pseudo-cyclostationnarité.

 de réalisation
de réalisation 
 , et
, et ![\begin{displaymath}
\esp{X\left(t\right)}=\sum_{k\in \mathbb{Z}} \sum_{m\in \ma...
...-\tau\right) e^{2\pi j\tau\left[n/T_{moy}+k f_m\right]} d\tau
\end{displaymath}](img838.png)
![\begin{displaymath}
\int_0^t r_m\left(t-\tau\right) e^{2\pi j\tau\left[l/T_{moy...
..._{moy}+k f_m\right]} e^{2\pi j t\left[n/T_{moy}+k f_m\right]}
\end{displaymath}](img839.png)

 modèle,
modèle,