- 3.2.1 Caractérisation à l'ordre 1
- 3.2.2 Caractérisation à l'ordre 2
- 3.2.3 Alternative dans le cas quasi-cyclostationnaire
La cyclostationnarité suppose l'existence de plusieurs réalisations d'un même processus. Or, en pratique, les signaux (issus d'une carte d'acquisition par exemple) correspondent à une seule réalisation de longueur finie. On va donc être conduit tout comme dans le cas stationnaire à parler d'ergodicité et d'estimation.
Le but de ce chapitre est dans un premier temps de généraliser la notion d'ergodicité aux processus cyclostationnaires et d'expliquer comment estimer les différentes grandeurs caractéristiques à l'ordre ![]() et
et ![]() . Dans un deuxième temps, un exemple de diagnostic sur les signaux d'engrenages illustre l'exploitation de la cyclostationnarité à l'ordre
. Dans un deuxième temps, un exemple de diagnostic sur les signaux d'engrenages illustre l'exploitation de la cyclostationnarité à l'ordre ![]() .
.
Lorsque l'on ne dispose que d'une seule réalisation, il existe deux solutions pour exploiter la cyclostationnarité.
Dans les deux cas, la réalisation devra contenir un grand nombre de cycles. Nous allons ici définir et utiliser l'approche cycloergodique, plus classique que celle de Gardner.
Comme la notion d'ergodisme fait appel à la notion de moyenne temporelle, la notion de cycloergodisme fera appel à la notion de moyenne cyclique ou synchrone.
Soit
![]() un processus stochastique cyclostationnaire complexe ou réel ayant comme période cyclique
un processus stochastique cyclostationnaire complexe ou réel ayant comme période cyclique ![]() , contenant un nombre de cycles important, et,
, contenant un nombre de cycles important, et,
![]() une réalisation
une réalisation ![]() particulière.
particulière.
On découpe le signal en ![]() blocs consécutifs de longueur
blocs consécutifs de longueur ![]() . La moyenne synchrone est alors donnée par :
. La moyenne synchrone est alors donnée par :
![\begin{displaymath}
\left<x\left(\theta\right)\right>_\Theta^K = \frac{1}{K} \s...
...^{K-1}x\left[mod\left(\theta + k \Theta,K\Theta\right)\right]
\end{displaymath}](img483.png) |
(3.1) |
Où
![]() est le reste de la division entière de
est le reste de la division entière de ![]() par
par ![]() . La fonction
. La fonction ![]() permet de définir la moyenne synchrone pour tout
permet de définir la moyenne synchrone pour tout ![]() . Cette opération est schématisée sur la figure
. Cette opération est schématisée sur la figure ![]() .
.
Puisque la moyenne synchrone extrait une composante périodique, qui admet une série de Fourier, elle peut être également écrite lorsque le nombre de blocs est infini :
Où le terme entre crochet représente la transformée de Fourier pour les fréquences
![]() et ses harmoniques. La composante périodique est ensuite générée par la série de Fourier. La moyenne synchrone apparaît donc comme un filtre en peigne sélectionnant uniquement la fréquence
et ses harmoniques. La composante périodique est ensuite générée par la série de Fourier. La moyenne synchrone apparaît donc comme un filtre en peigne sélectionnant uniquement la fréquence ![]() et ses multiples.
et ses multiples.
Soit un processus stochastique cyclique
![]() de période cyclique
de période cyclique ![]() , la
, la
![]() réalisation de ce processus
réalisation de ce processus
![]() , et une fonction certaine
, et une fonction certaine ![]() .
.
![]() est cycloergodique au sens fort à la période cyclique
est cycloergodique au sens fort à la période cyclique ![]() si la moyenne synchrone (cyclique)
si la moyenne synchrone (cyclique)
![]() converge presque sûrement3.1 vers un signal certain quand
converge presque sûrement3.1 vers un signal certain quand ![]() tend vers l'infini.
tend vers l'infini.
Si le processus
![]() est de plus cyclostationnaire à la période cyclique
est de plus cyclostationnaire à la période cyclique ![]() , ce signal certain correspond au moment d'ordre
, ce signal certain correspond au moment d'ordre ![]() du processus
du processus
![]() pour
pour
![]() .
.
En pratique, la cycloergodicité sera supposée (ou établie d'après un modèle). En effet, la vérifier nécessite de posséder différentes réalisations.
Dans le cas polycyclostationnaire, le signal n'a pas de période mais plusieurs ``périodes'' incommensurables entre elles. Chacune des périodes produit un peigne de Dirac dans le domaine fréquentiel. Puisque ces périodes sont incommensurables, tous les peignes sont distincts. Dès lors, la moyenne synchrone agit comme un filtre en peigne et, permet de sélectionner uniquement la période ![]() prise comme référence.
prise comme référence.
Afin de définir la cycloergodicité dans ce contexte, nous allons définir l'extracteur des composantes poly-périodiques associées aux K périodes cycliques
![]() :
:
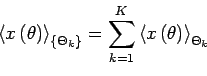 |
(3.3) |
Nous pouvons alors définir le cycloergodisme pour plusieurs fréquences cycliques :
Soit un processus stochastique poly-cyclique
![]() de périodes cycliques
de périodes cycliques
![]() ,
,
![]()
![]() réalisation de ce processus, et une fonction certaine
réalisation de ce processus, et une fonction certaine ![]() .
.
![]() est poly-cycloergodique au sens fort aux périodes cycliques
est poly-cycloergodique au sens fort aux périodes cycliques
![]() si
si
![]() converge presque sûrement vers un signal certain.
converge presque sûrement vers un signal certain.
L'introduction du cycloergodisme va nous permettre de développer les estimateurs basés sur une réalisation
![]() d'un processus cycloergodique
d'un processus cycloergodique
![]() afin de caractériser la cyclostationnarité aux ordres
afin de caractériser la cyclostationnarité aux ordres ![]() et
et ![]() .
.
Les estimations, basées sur une seule réalisation, peuvent également être réalisées en supposant l'unicité du processus générateur pour chacun des cycles considérés. Sous cette hypothèse, il est possible d'assimiler un cycle à une réalisation c'est à dire de substituer une moyenne d'ensemble par une moyenne de cycle.
Pour caractériser la cyclostationnarité à l'ordre ![]() , nous allons chercher à estimer la composante (presque) périodique d'un signal (presque) cyclostationnaire.
, nous allons chercher à estimer la composante (presque) périodique d'un signal (presque) cyclostationnaire.
Le premier outil destiné à extraire cette composante périodique est la moyenne synchrone [#!braun:extraction!#] qui nous a servi à introduire la cycloergodicité dans le paragraphe précédent. La moyenne synchrone, bien qu'en apparence simple à calculer présente quelques pièges :
Dans, un tel cas où les fréquences d'entrée et de sortie sont commensurables (rapport ![]() ,
, ![]() et
et ![]() entiers), il suffit tout simplement de sur-échantillonner d'un facteur
entiers), il suffit tout simplement de sur-échantillonner d'un facteur ![]() et de le sous-échantillonner d'un facteur
et de le sous-échantillonner d'un facteur ![]() afin d'obtenir un nombre de points entier par tour de l'arbre de sortie (les outils de conversion de fréquence d'échantillonnage sont décrits dans [#!crochiere:multirate!#]). Il est également possible d'utiliser une interpolation pour effectuer le ré-échantillonnage.
afin d'obtenir un nombre de points entier par tour de l'arbre de sortie (les outils de conversion de fréquence d'échantillonnage sont décrits dans [#!crochiere:multirate!#]). Il est également possible d'utiliser une interpolation pour effectuer le ré-échantillonnage.
Ces conditions tendent à favoriser l'échantillonnage angulaire qui fournit un nombre de points constant par tour de l'arbre de référence (suppression de l'effet des fluctuations de vitesses). Des méthodes permettant de transformer des signaux à variable générique temporelle en signaux à variable générique angulaire ont été proposées au chapitre ![]() . En angulaire, les signaux sont ``synchronisés'' par rapport à la période cyclique.
. En angulaire, les signaux sont ``synchronisés'' par rapport à la période cyclique.
Il est possible d'écrire la moyenne synchrone sous une forme similaire à l'équation (![]() ) pour un signal de longueur
) pour un signal de longueur ![]() , multiple de la taille d'un bloc de
, multiple de la taille d'un bloc de ![]() échantillons :
échantillons :
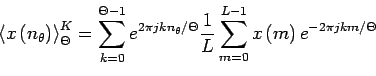 |
(3.4) |
A la différence du cas continu, le nombre de points fini, conduira à employer un filtre en peigne avec des ``dents élargies''. On ne sélectionnera donc plus aussi précisément une fréquence donnée. La réponse fréquentielle du filtre en peigne équivalent est donnée par [#!braun:extraction2!#]:
 |
(3.5) |
Cette réponse est une fonction de Dirichlet qui a un maximum à la fréquence ![]() ainsi qu'à ses harmoniques (voir figure
ainsi qu'à ses harmoniques (voir figure ![]() ). La largeur des dents est inversement proportionnelle au nombre de cycles
). La largeur des dents est inversement proportionnelle au nombre de cycles ![]() . Dès lors, plus le nombre de cycles est grand, plus le filtre sera sélectif. Quand le nombre de cycles tend vers l'infini, ce filtre tend vers le filtre en peigne de l'équation (
. Dès lors, plus le nombre de cycles est grand, plus le filtre sera sélectif. Quand le nombre de cycles tend vers l'infini, ce filtre tend vers le filtre en peigne de l'équation (![]() ).
).
La moyenne synchrone étant calculée sur un nombre fini de points, il n'est pas toujours facile de pouvoir différencier une composante ``synchrone'' qui ressortira grâce au moyennage constructif, d'une composante asynchrone subissant un moyennage destructif. Nous avons alors proposé dans [#!bonnardot:aide!#] d'utiliser un critère afin de détecter les valeurs résultant d'un moyennage constructif. Ce dernier est intéressant lorsque la composante périodique a une amplitude faible vis à vis du signal ou que le nombre de cycles utilisés pour le moyennage est faible. Lorsque le nombre de cycles est important (quelques centaines), le bruit est réduit fortement, alors un examen visuel du signal est souvent suffisant.
Ce critère est basé sur la définition d'un seuil. Toute valeur au dessus de ce seuil sera considérée comme une composante synchrone (avec un risque de se tromper donné).
La moyenne synchrone dépend de l'angle, donc le seuil en dépendra également. Pour définir un tel seuil, nous modélisons le signal comme la somme d'une composante déterministe
![]() de période
de période ![]() et d'une composante résiduelle
et d'une composante résiduelle
![]() incluant le bruit ainsi que les contributions cyclostationnaires aux ordres supérieurs. Le signal devra avoir une composante continue nulle, c'est-à-dire
incluant le bruit ainsi que les contributions cyclostationnaires aux ordres supérieurs. Le signal devra avoir une composante continue nulle, c'est-à-dire
![]() . Cette condition n'est pas restrictive puisque l'on s'intéresse uniquement à la partie synchrone. On pourra également si besoin est, rajouter la moyenne classique au seuil et au signal après traitement.
. Cette condition n'est pas restrictive puisque l'on s'intéresse uniquement à la partie synchrone. On pourra également si besoin est, rajouter la moyenne classique au seuil et au signal après traitement.
| (3.6) |
Où la moyenne synchrone calculée sur ![]() cycles est
cycles est
![]() .
.
Soit
![]() , le signal obtenu en gardant les échantillons distants de
, le signal obtenu en gardant les échantillons distants de ![]() à partir de
à partir de ![]() . Nous supposerons pour établir le seuil que pour un angle
. Nous supposerons pour établir le seuil que pour un angle ![]() donné,
donné,
![]() suit une loi normale de moyenne
suit une loi normale de moyenne
![]() et d'écart type
et d'écart type
![]() . Après moyennage synchrone,
. Après moyennage synchrone,
![]() suivra donc une loi normale de moyenne
suivra donc une loi normale de moyenne
![]() et d'écart type
et d'écart type
![]() .
.
L'écart type de
![]() notée
notée
![]() sera estimée sur
sera estimée sur ![]() cycles par :
cycles par :
![\begin{displaymath}
\hat{\sigma}_b\left(\theta\right)=\sqrt{\frac{K}{K-1}\left<...
...a\right)-\hat{m}\left(\theta\right)\right]^2\right>_\Theta^K}
\end{displaymath}](img519.png) |
(3.7) |
Nous allons ensuite tester si
![]() , c'est-à-dire si la moyenne synchrone existe pour un angle donné. Étant donné que l'on utilise un estimateur pour l'écart type, la quantité
, c'est-à-dire si la moyenne synchrone existe pour un angle donné. Étant donné que l'on utilise un estimateur pour l'écart type, la quantité
![]() suivra une loi de Student
suivra une loi de Student ![]() à
à ![]() degrés de liberté.
degrés de liberté.
Pour valider l'hypothèse
![]() cyclostationnaire à l'ordre
cyclostationnaire à l'ordre ![]() avec un risque de se tromper de
avec un risque de se tromper de ![]() , on exigera :
, on exigera :
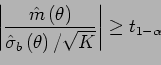 |
(3.8) |
On ne peut rien conclure si le signal est en dessous du seuil : il s'agit soit de bruit, soit d'une moyenne synchrone trop faible (auquel cas il faut augmenter le nombre de cycles).
Cette approche peut être discutable en présence de défauts puisque le kurtosis (c'est-à-dire la non gaussianité) de la série
![]() a été utilisée pour bâtir un indicateur de défaut [#!raad:contributions!#]. Néanmoins, elle reste pertinente avant et lors de l'apparition du défaut, car une fois le défaut établi, le seuil n'est plus utile puisque ce défaut devient clairement identifiable dans la moyenne synchrone.
a été utilisée pour bâtir un indicateur de défaut [#!raad:contributions!#]. Néanmoins, elle reste pertinente avant et lors de l'apparition du défaut, car une fois le défaut établi, le seuil n'est plus utile puisque ce défaut devient clairement identifiable dans la moyenne synchrone.
La figure ![]() illustre l'utilisation du seuil. La figure (a) montre un cycle d'un signal accéléromètrique issu d'un engrenage auquel un bruit gaussien a été ajouté afin de bien mettre en évidence le rôle du seuil.
illustre l'utilisation du seuil. La figure (a) montre un cycle d'un signal accéléromètrique issu d'un engrenage auquel un bruit gaussien a été ajouté afin de bien mettre en évidence le rôle du seuil.
La figure (b) montre la moyenne synchrone et le seuil associé, calculés sur ![]() tours. Étant donné le nombre de cycles, on obtient un seuil très bas. Ce signal pourra donc être considéré comme étant la composante périodique. Il sera comparé au signal (c) qui est une moyenne synchrone sur
tours. Étant donné le nombre de cycles, on obtient un seuil très bas. Ce signal pourra donc être considéré comme étant la composante périodique. Il sera comparé au signal (c) qui est une moyenne synchrone sur ![]() tours. Le seuil qui est ici beaucoup plus élevé, va indiquer une zone correspondant à une moyenne synchrone nulle avec un risque de se tromper de
tours. Le seuil qui est ici beaucoup plus élevé, va indiquer une zone correspondant à une moyenne synchrone nulle avec un risque de se tromper de ![]() . En conséquence, toute valeur à l'intérieur de la zone pourra être nulle et ne sera pas interprétable (ceci est facilement vérifiable en comparant les courbes (b) et (c) aux alentours du
. En conséquence, toute valeur à l'intérieur de la zone pourra être nulle et ne sera pas interprétable (ceci est facilement vérifiable en comparant les courbes (b) et (c) aux alentours du
![]() échantillon).
échantillon).
La courbe (d) suggère une autre utilisation du seuil : la détection de cyclostationnarité. Pour cette courbe, une période de 502 points a été utilisée au lieu de 512 points (1 tour). Dès lors, on a un signal qui n'est plus cyclostationnaire à l'ordre 1 pour la période cyclique 502. Il est donc naturellement en dessous du seuil. En tirant parti de cette remarque, il est alors possible en comptabilisant le pourcentage de signal au-dessus du seuil pour différentes périodes de détecter le ou les cycles présents dans le signal. Cette utilisation est suggérée à titre indicatif puisqu'il existe de meilleurs outils pour trouver les fréquences cycliques (cepstre, corrélation spectrale, ...).
Il convient de distinguer deux cas:
Pour illustrer ce biais nous avons construit sur la figure ![]() un signal composé de la somme d'une composante périodique
un signal composé de la somme d'une composante périodique
![]() de période
de période ![]() échantillons et d'une autre composante périodique
échantillons et d'une autre composante périodique
![]() de période
de période ![]() échantillons. Le maximum de chacune des composantes est d'amplitude unitaire. La période commune du signal est alors
échantillons. Le maximum de chacune des composantes est d'amplitude unitaire. La période commune du signal est alors
![]() échantillons. La figure
échantillons. La figure ![]() montre la moyenne synchrone calculée relativement à la période
montre la moyenne synchrone calculée relativement à la période ![]() .
.
La moyenne synchrone calculée sur une durée infinie de période commune est formée du motif récurrent de
![]() (flèche notée C) que l'on souhaitait isoler mais également de
(flèche notée C) que l'on souhaitait isoler mais également de ![]() motifs récurents issus de
motifs récurents issus de
![]() dont l'amplitude a été divisée par quatre (flèches notées D). En effet, dans un cycle commun, il y a
dont l'amplitude a été divisée par quatre (flèches notées D). En effet, dans un cycle commun, il y a ![]() motifs issus de
motifs issus de
![]() qui subissent un moyennage constructif et
qui subissent un moyennage constructif et ![]() motifs issus de
motifs issus de
![]() qui subissent un moyennage destructif (ce qui explique leur amplitude de 0.25).
qui subissent un moyennage destructif (ce qui explique leur amplitude de 0.25).
A l'ordre ![]() , il est possible d'utiliser
, il est possible d'utiliser ![]() représentations pour caractériser la
représentations pour caractériser la ![]() . Chaque représentation est liée soit à un repère angulaire, soit à un repère fréquentiel associé
. Chaque représentation est liée soit à un repère angulaire, soit à un repère fréquentiel associé ![]() soit à un repère mixte. Pour le repère angulaire nous utiliserons l'angle
soit à un repère mixte. Pour le repère angulaire nous utiliserons l'angle ![]() ainsi que le retard
ainsi que le retard ![]() pour la corrélation. Bien que classiquement le domaine fréquentiel soit gradué en
pour la corrélation. Bien que classiquement le domaine fréquentiel soit gradué en ![]() , l'utilisation d'une telle graduation pour des signaux dépendant de l'angle nécessite quelques approximations. Dans le domaine angulaire, le nombre de points par tour
, l'utilisation d'une telle graduation pour des signaux dépendant de l'angle nécessite quelques approximations. Dans le domaine angulaire, le nombre de points par tour ![]() est constant. Pour deux fréquences de rotation distinctes, la quantité
est constant. Pour deux fréquences de rotation distinctes, la quantité ![]() restera constante. Dès lors, on ne pourra plus appeler cette quantité une fréquence. La quantité
restera constante. Dès lors, on ne pourra plus appeler cette quantité une fréquence. La quantité ![]() sera alors appelé un ordre [#!bruel:order!#], l'ordre
sera alors appelé un ordre [#!bruel:order!#], l'ordre ![]() correspond à
correspond à ![]() fois la fréquence de rotation instantanée. L'échelle fréquentielle en
fois la fréquence de rotation instantanée. L'échelle fréquentielle en ![]() étant en général plus familière, il sera toutefois possible de l'utiliser si les variations de vitesse sont faibles autour d'une vitesse de rotation moyenne constante, nous aurons alors
étant en général plus familière, il sera toutefois possible de l'utiliser si les variations de vitesse sont faibles autour d'une vitesse de rotation moyenne constante, nous aurons alors ![]() (de l'ordre de quelques pour cent ou pour mille autour de la fréquence de rotation moyenne). Il est bien sûr nécessaire de mesurer au préalable la vitesse de rotation moyenne.
(de l'ordre de quelques pour cent ou pour mille autour de la fréquence de rotation moyenne). Il est bien sûr nécessaire de mesurer au préalable la vitesse de rotation moyenne.
Pour définir un spectre, il est nécessaire de calculer la transformée de Fourier du signal. Malheureusement, la transformation de Fourier définie par
![]() n'est pas convergente, en moyenne quadratique lorsque
n'est pas convergente, en moyenne quadratique lorsque
![]() est un signal aléatoire. Il convient alors d'utiliser la décomposition de Cramér présentée dans [#!cramer:mathematical!#,#!blanc:theorie!#] :
est un signal aléatoire. Il convient alors d'utiliser la décomposition de Cramér présentée dans [#!cramer:mathematical!#,#!blanc:theorie!#] :
 |
(3.9) |
Où
![]() est l'incrément spectral à la fréquence
est l'incrément spectral à la fréquence ![]() . Pour
. Pour
![]() centré (approche cumulant), on a :
centré (approche cumulant), on a :
où
![]() est une mesure de puissance qui quantifie l'interaction entre les deux canaux
est une mesure de puissance qui quantifie l'interaction entre les deux canaux ![]() et
et ![]() telle que :
telle que :
La mesure
![]() est une différentielle au second ordre d'une fonction certaine
est une différentielle au second ordre d'une fonction certaine
![]() homogène à une distribution spectrale de la fonction d'autocovariance
homogène à une distribution spectrale de la fonction d'autocovariance
![]() . Par suite, on admettra qu'il existe une densité de corrélation spectrale (DCS)
. Par suite, on admettra qu'il existe une densité de corrélation spectrale (DCS)
![]() telle que :
telle que :
La DCS dépend alors de deux fréquences et s'identifie à un spectre lorsque ces dernières sont identiques :
![]() , et, dans le cas général, à l'inter-spectre entre deux versions décalées dans le domaine fréquentiel de
, et, dans le cas général, à l'inter-spectre entre deux versions décalées dans le domaine fréquentiel de
![]() :
:
![]() .
.
Dans le cas cyclostationnaire, la périodicité du cumulant d'ordre ![]() :
:
![]() appliquée aux équations (
appliquée aux équations (![]() ) et (
) et (![]() ) impliquera :
) impliquera :
0
Soit :
 |
(3.15) |
La mesure de puissance sera donc nulle partout sauf sur l'ensemble des droites d'équation
![]() (cf. figure
(cf. figure ![]() ). Il apparaît alors intéressant de faire le changement de repère :
). Il apparaît alors intéressant de faire le changement de repère :
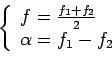 |
(3.16) |
Ce changement de repère permet de faire apparaître la fréquence cyclique ![]() . Cette fréquence cyclique prend tout son sens en réécrivant l'équation
. Cette fréquence cyclique prend tout son sens en réécrivant l'équation ![]() dans ce nouveau repère :
dans ce nouveau repère :
La DCS apparaît donc comme le produit de deux versions décalées en fréquence d'une quantité ![]() des incréments spectraux à la fréquence
des incréments spectraux à la fréquence ![]() . Une valeur non nulle de la DCS caractérisera donc un lien entre les fréquences
. Une valeur non nulle de la DCS caractérisera donc un lien entre les fréquences
![]() et
et
![]() .
.
On peut extraire la partie intéressante de cette mesure de puissance en définissant la densité spectrale cyclique (DSC) qui correspond aux valeurs non nulles de la DCS :
La densité de corrélation est alors continue par rapport à la variable ![]() et discrète par rapport à la fréquence cyclique
et discrète par rapport à la fréquence cyclique ![]() . Ce résultat est une propriété remarquable des signaux cyclostationnaires.
. Ce résultat est une propriété remarquable des signaux cyclostationnaires.
L'équation (![]() ) est la forme symétrique de la DCS. Il existe également une forme assymétrique définie par :
) est la forme symétrique de la DCS. Il existe également une forme assymétrique définie par :
| (3.19) |
L'estimation de la corrélation spectrale se fera en deux étapes comme l'indique la figure ![]() :
:
Comme la corrélation spectrale est basée sur le calcul d'un interspectre, on utilisera les mêmes techniques d'estimation : le périodogramme moyenné et le périodogramme lissé.
La figure ![]() illustre ces deux techniques.
illustre ces deux techniques.
La méthode du périodogramme moyenné est basée sur le découpage du signal en ![]() blocs de
blocs de ![]() points. La corrélation spectrale est tout d'abord calculée sur chacun de ces blocs. Les corrélations spectrales ainsi obtenues sont ensuite moyennées.
points. La corrélation spectrale est tout d'abord calculée sur chacun de ces blocs. Les corrélations spectrales ainsi obtenues sont ensuite moyennées.
La méthode du périodogramme lissé est basée sur le lissage d'une corrélation spectrale calculée sur le signal complet. On sous-échantillonne ensuite cette image selon l'axe fréquentiel.
D'après les calculs de complexité de [#!bouillaut:approches!#], la méthode du périodogramme moyenné devient plus avantageuse à partir de ![]() moyennes, de plus, elle nécessite moins de mémoire.
moyennes, de plus, elle nécessite moins de mémoire.
Lors de l'utilisation du périodogramme moyenné, il faudra prendre garde à la méthode d'évaluation de l'interspectre. En effet, dans les logiciels comme Matlab, la transformée de Fourier est calculée en considérant que chacun des blocs débute à un instant nul (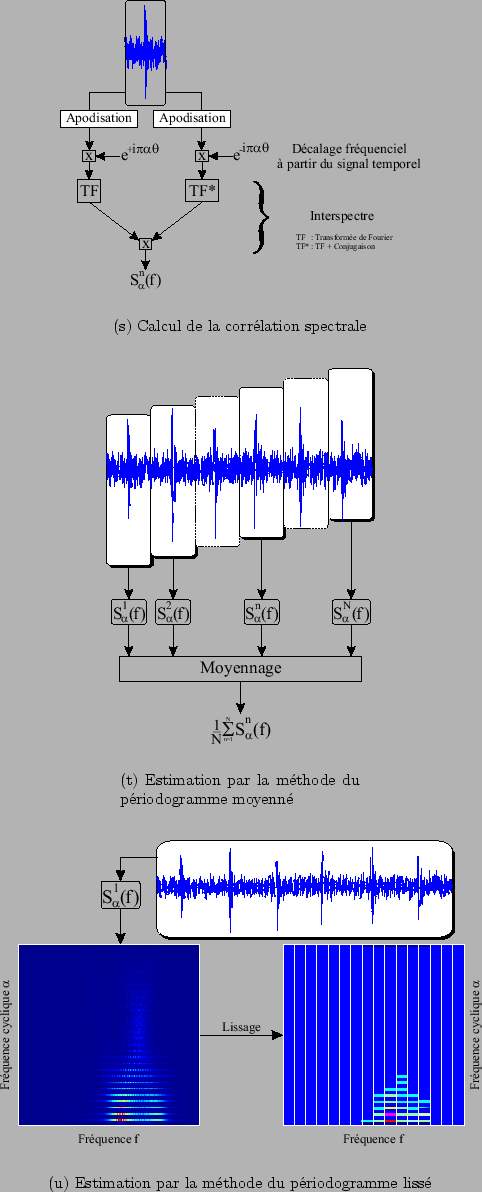 ). Dès lors, pour la
). Dès lors, pour la
![]() tranche, on introduira un déphasage de
tranche, on introduira un déphasage de
![]() [#!capdessus:aide!#] qu'il suffira de compenser pour estimer correctement la corrélation spectrale.
[#!capdessus:aide!#] qu'il suffira de compenser pour estimer correctement la corrélation spectrale.
Le périodogramme moyenné conduit à faire un compromis entre le biais et la résolution fréquentielle. En effet, le signal étant de taille finie, si l'on augmente le nombre de blocs on diminue le biais, mais, un bloc de taille réduite conduit à une résolution fréquentielle plus faible.
Un dilemme biais variance apparaît pour l'estimateur basé sur le périodogramme lissé lors du choix de la fenêtre de lissage : une fenêtre de lissage de durée importante permet de réduire le biais mais la variance dépend de la forme de cette fenêtre.
Signaux presque-cyclostationnaires
Dans le cas presque-cyclostationnaire, le cumulant d'ordre ![]() peut être approximé uniformément par un polynôme trigonométrique de la forme :
peut être approximé uniformément par un polynôme trigonométrique de la forme :
Cette formulation conduira à une mesure de puissance nulle partout sauf sur l'ensemble des droites d'équation 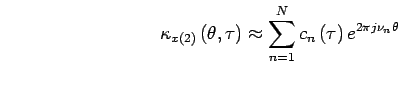 . La figure
. La figure ![]() montre ce support pour un signal constitué de deux pseudo-périodes cycliques ainsi que de leurs harmoniques. Dès lors, les valeurs de la DSC non nulles correspondront non plus à une fréquence cyclique et à ces harmoniques mais à l'ensemble des pseudo-périodes
montre ce support pour un signal constitué de deux pseudo-périodes cycliques ainsi que de leurs harmoniques. Dès lors, les valeurs de la DSC non nulles correspondront non plus à une fréquence cyclique et à ces harmoniques mais à l'ensemble des pseudo-périodes
![]() (incluant les harmoniques).
(incluant les harmoniques).
Parmi les applications de la DSC, on pourra citer le degré de cyclostationnarité introduit par Gardner et repris dans [#!zivanovic:degree!#] :
 |
(3.21) |
Ce degré de cyclostationnarité peut être interprété comme la distance avec le processus stationnaire le plus proche [#!gardner:characterization!#]. Une étude et une généralisation des mesures de cyclostationnarité aux ordres supérieurs pourront être trouvés dans [#!raad:contributions!#].
L'autocovariance correspond au cumulant d'ordre 2. Puisqu'elle est périodique dans le contexte cyclostationnaire:
 , il est classique de faire le changement de repère:
, il est classique de faire le changement de repère:
| (3.22) |
On utilise également la variance synchrone définie par
 qui correspond à la puissance instantanée du système.
qui correspond à la puissance instantanée du système.
Cas cyclostationnaire
Dans le cas cyclostationnaire on a
![]() quels que soient les entiers
quels que soient les entiers ![]() et
et ![]() . L'autocovariance admet donc un développement en série de Fourier dont les coefficients sont donnés par :
. L'autocovariance admet donc un développement en série de Fourier dont les coefficients sont donnés par :
Où les fréquences cycliques ![]() sont multiples de la fréquence de base du système :
sont multiples de la fréquence de base du système :
 , k entier.
, k entier.
La fonction
![]() est alors appelée fonction d'autocovariance cyclique. Elle est reliée à la DSC par :
est alors appelée fonction d'autocovariance cyclique. Elle est reliée à la DSC par :
| (3.24) |
Cas presque-cyclostationnaire
Dans le cas presque-cyclostationnaire la variance peut être approximée par un polynôme trigonométrique qui admet une décomposition de Fourier-Bohr (équation ![]() ). Ce polynôme fournit directement la valeur de la variance cyclique :
). Ce polynôme fournit directement la valeur de la variance cyclique :
 .
.
A la différence du cas cyclostationnaire où l'ensemble des valeurs ![]() correspondait au fondamental et à ses harmoniques, elles correspondent ici à un ensemble de fréquences données.
correspondait au fondamental et à ses harmoniques, elles correspondent ici à un ensemble de fréquences données.
La variance cyclique sera alors reliée à la DSC par :
| (3.25) |
L'égalité ne peut pas être utilisée ici car le polynôme trigonométrique approche seulement la variance.
Nous traitons ici des signaux stochastiques. Or, la distribution de Wigner-Ville
![]() a été originellement conçue pour des signaux déterministes d'énergie finie par :
a été originellement conçue pour des signaux déterministes d'énergie finie par :
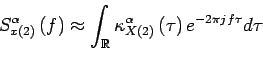 |
(3.26) |
 qui est défini comme l'espérance mathématique de la distribution de Wigner-Ville du processus aléatoire centré. Ainsi, pour un processus aléatoire
qui est défini comme l'espérance mathématique de la distribution de Wigner-Ville du processus aléatoire centré. Ainsi, pour un processus aléatoire
| (3.27) |
Sous réserve de commutativité entre l'espérance et l'intégration, il est possible de lier l'autocovariance et le spectre de Wigner-Ville par :
Lorsque le processus stochastique
![]() est (pseudo)-cyclostationnaire, le spectre de Wigner-Ville présente une structure (pseudo)-périodique suivant la variable angulaire
est (pseudo)-cyclostationnaire, le spectre de Wigner-Ville présente une structure (pseudo)-périodique suivant la variable angulaire ![]() .
.
En combinant les équations (![]() ) et (
) et (![]() ), on peut écrire :
), on peut écrire :
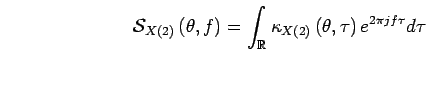 |
(3.29) | ||
 |
(3.30) |
Dans le cas cyclostationnaire, on aura
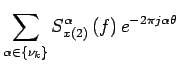 . Dans le cas presque-cyclostationnaire, les fréquences
. Dans le cas presque-cyclostationnaire, les fréquences ![]() ne seront pas forcément multiples entre elles, de plus, il conviendra de remplacer l'égalité par une approximation.
ne seront pas forcément multiples entre elles, de plus, il conviendra de remplacer l'égalité par une approximation.
Cette équation établit le lien entre le spectre de Wigner-Ville et la DSC.
La figure ![]() résume les relations entre les différentes représentations à l'ordre
résume les relations entre les différentes représentations à l'ordre ![]() .
.
Lorsque les signaux sont quasi-cyclostationnaires (il existe des périodes incommensurables entre elles), il est possible d'utiliser l'opérateur d'extraction de composante périodique
 défini par l'équation (
défini par l'équation (![]() ).
).
Comme indiqué précédemment, cet opérateur apparaît comme un filtre en peigne sélectionnant uniquement les composantes de période ![]() .
.
On peut alors généraliser cet opérateur à l'ordre 2 par :
| (3.31) |
Nous avons proposé ici deux méthodes pour traiter le cas presque cyclostationnaire : soit de prendre en considération et obtenir des statistiques presque-cyclostationnaires, soit extraire chaque période (sous réserve d'existence c'est-à-dire de quasi-cyclostationnarité) et travailler alors sur des signaux cyclostationnaires. Le choix de la méthode dépendra alors du type de signal et des traitements que l'on veut faire. Par exemple, si chaque période a une signification physique, la dernière méthode deviendra intéressante.
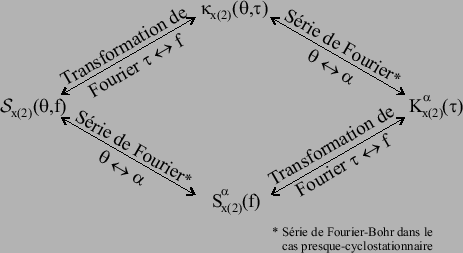
Ce paragraphe a pour but de montrer un exemple d'exploitation de la cyclostationnarité pour le diagnostic de défaut d'engrenages. Les signaux accéléromètriques ont été acquis au centre d'études et recherches EDF à Chatou sur un banc d'essai de fatigue. Ces signaux ont notamment été exploités dans [#!fontanive:surveillance!#] et [#!elbadaoui:contribution!#]. Nous proposons ici une autre analyse basée sur la cyclostationnarité.
Il s'agit d'un banc d'essai composé d'une roue de ![]() dents et d'une autre de
dents et d'une autre de ![]() dents. La fréquence de rotation de la roue menante est de
dents. La fréquence de rotation de la roue menante est de ![]() et la fréquence d'échantillonnage de
et la fréquence d'échantillonnage de ![]() . Afin d'étudier l'apparition d'un défaut, un essai de fatigue a été réalisé. Tout au long de cet essai 15 acquisitions ont été faites. Un défaut de type écaillage a été détecté à partir de la dixième mesure. Le défaut s'est aggravé progressivement jusqu'à la rupture d'une dent lors du quinzième relevé.
. Afin d'étudier l'apparition d'un défaut, un essai de fatigue a été réalisé. Tout au long de cet essai 15 acquisitions ont été faites. Un défaut de type écaillage a été détecté à partir de la dixième mesure. Le défaut s'est aggravé progressivement jusqu'à la rupture d'une dent lors du quinzième relevé.
Dans les précédentes publications, le défaut a été détecté lors du
![]() essai. Par ailleurs, les signaux ont été qualifiés de ``fortement bruités''. Nous allons, en exploitant la cyclostationnarité retrouver ces mêmes résultats. Pour cela, nous avons préalablement re-échantillonné les signaux dans le domaine angulaire en estimant la phase instantanée par démodulation autour de deux fois la fréquence d'engrènement.
essai. Par ailleurs, les signaux ont été qualifiés de ``fortement bruités''. Nous allons, en exploitant la cyclostationnarité retrouver ces mêmes résultats. Pour cela, nous avons préalablement re-échantillonné les signaux dans le domaine angulaire en estimant la phase instantanée par démodulation autour de deux fois la fréquence d'engrènement.
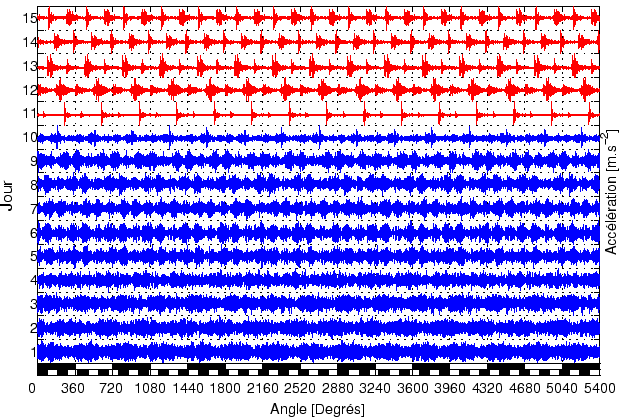
La figure ![]() montre les
montre les ![]() acquisitions pendant une durée correspondant à la période commune (intervalle au bout duquel l'engrenage revient dans la même configuration (mêmes dents en contact). La période commune
acquisitions pendant une durée correspondant à la période commune (intervalle au bout duquel l'engrenage revient dans la même configuration (mêmes dents en contact). La période commune ![]() représente
représente ![]() tours de la roue de
tours de la roue de ![]() dents ou
dents ou ![]() tours de la roue de
tours de la roue de ![]() dents (15 et 56 n'ayant pas de multiple commun). Chacun des signaux a été normalisé par rapport à leur valeur crête-à-crête avant affichage afin de faciliter leur comparaison. Le défaut apparaît nettement le
dents (15 et 56 n'ayant pas de multiple commun). Chacun des signaux a été normalisé par rapport à leur valeur crête-à-crête avant affichage afin de faciliter leur comparaison. Le défaut apparaît nettement le
![]() jour alors qu'il avait été détecté par un expert le
jour alors qu'il avait été détecté par un expert le
![]() jour.
jour.
En toute rigueur les signaux d'engrenage sont cyclostationnaires, c'est-à-dire qu'il existe une période cyclique. Cette période correspond au cycle commun de l'engrenage. Nous avons préféré les qualifier de polycyclostationnaires puisque physiquement cette période est composée de ``sous'' périodes correspondant aux périodes de rotation des roues qui sont dans un rapport rationnel, il serait alors dommage de ne pas exploiter ces informations. Nous allons exploiter la moyenne synchrone sur la période commune ![]() afin d'examiner l'apparition au dixième jour.
afin d'examiner l'apparition au dixième jour.
Si on considère le signal cyclostationnaire à l'ordre ![]() , on le modélise sous la forme :
, on le modélise sous la forme :
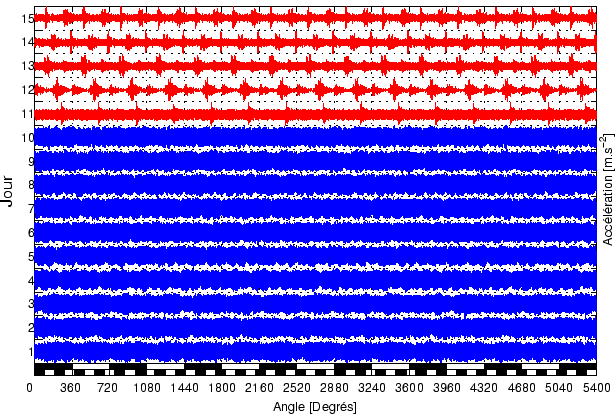 |
(3.32) |
Où
![]() est un signal périodique de période
est un signal périodique de période ![]() que l'on estimera à l'aide d'une moyenne synchrone. Le signal ne contient malheureusement que
que l'on estimera à l'aide d'une moyenne synchrone. Le signal ne contient malheureusement que ![]() blocs de taille
blocs de taille ![]() . La figure
. La figure ![]() montre l'estimation de cette période commune, le résidu est présenté sur la figure
montre l'estimation de cette période commune, le résidu est présenté sur la figure ![]() . On peut constater que la période commune est très proche du signal et que le résidu n'apporte que peu d'information nouvelle.
. On peut constater que la période commune est très proche du signal et que le résidu n'apporte que peu d'information nouvelle.
Devant l'insuccès de l'approche cyclostationnaire, nous allons utiliser une approche polycyclostationnaire. Pour cela le signal sera modélisé par :
 |
(3.33) |
Où le signal est composé de deux signaux périodiques
![]() de période
de période ![]() et
et
![]() de période
de période ![]() dont la période correspond respectivement à la
dont la période correspond respectivement à la
![]() et à la
et à la
![]() roue ; de
roue ; de
![]() de période
de période ![]() correspondant à l'interaction des
correspondant à l'interaction des ![]() roues ; d'un signal résiduel
roues ; d'un signal résiduel
![]() non périodique. Nous supposerons que les périodes
non périodique. Nous supposerons que les périodes ![]() et
et ![]() ne sont pas multiples entre elles mais dans un rapport rationnel. Dans le cas contraire, cette approche n'aurait aucun intérêt.
ne sont pas multiples entre elles mais dans un rapport rationnel. Dans le cas contraire, cette approche n'aurait aucun intérêt.
La composante précédemment estimée,
![]() correspond à la somme des trois composantes périodiques. L'estimation de
correspond à la somme des trois composantes périodiques. L'estimation de
![]() se fera en calculant la moyenne synchrone
se fera en calculant la moyenne synchrone
![]() .
.
Malheureusement, l'estimateur de
![]() est biaisé. En effet, comme
est biaisé. En effet, comme
![]() est périodique d'une part et que
est périodique d'une part et que ![]() est sous-multiple de cette période, une moyenne synchrone calculée sur un nombre infini de blocs fera toujours apparaître un nombre fini
est sous-multiple de cette période, une moyenne synchrone calculée sur un nombre infini de blocs fera toujours apparaître un nombre fini
![]() de composantes décalées de
de composantes décalées de
![]() lors du moyennage :
lors du moyennage :
| (3.34) |
Où :
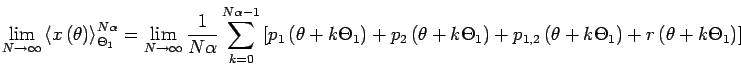 correspondra, par définition à
correspondra, par définition à
Soit :
| (3.35) |
Néanmoins, si les nombres de dents sont élevés et qu'ils sont premiers entre eux, le nombre ![]() sera également élevé. Il est tout de même important de noter que l'estimateur de
sera également élevé. Il est tout de même important de noter que l'estimateur de
![]() est quoiqu'il en soit biaisé.
est quoiqu'il en soit biaisé.
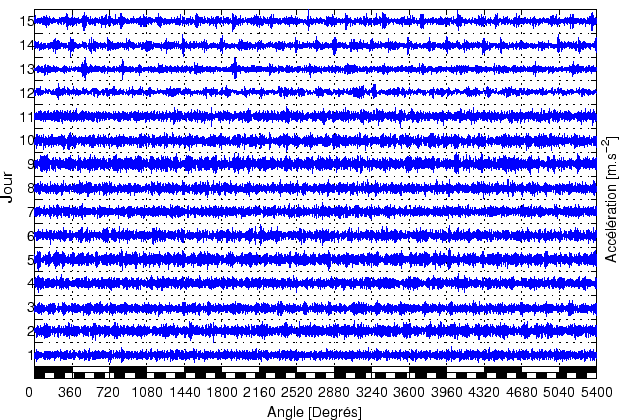
Pour l'engrenage de EDF, nous allons essayer d'évaluer la moyenne associée à l'arbre 1 :
 |
(3.36) |
Pour cela, nous avons évalué la moyenne synchrone suivant la période commune, pour estimer la contribution :
| (3.37) |
Puis nous avons retranché
![]() estimé par moyennage synchrone sur une période
estimé par moyennage synchrone sur une période ![]() (
(![]() ). Le résultat est présenté sur la figure
). Le résultat est présenté sur la figure ![]() .
.
Bien que l'estimation soit biaisée
 , le défaut est nettement visible et au
, le défaut est nettement visible et au
![]() jour (il se manifeste par l'apparition de pics dans le signal).
jour (il se manifeste par l'apparition de pics dans le signal).
Ce signal a été qualifié de fortement bruité, nous avons établi ici que cette source de bruit provenait de la contribution de la deuxième roue. Cette composante, fortement énergétique lors des premières acquisitions masque les premiers signes de l'apparition du défaut. Lorsque le défaut progresse, l'énergie associée à la roue 1 porteuse du défaut devient plus importante et le fait ainsi ressortir sur le signal non traité.
De nombreuses autres approches ou méthodes complémentaires pourront être envisagées. Nous nous sommes néanmoins limités à cette dernière puisqu'elle est très simple et qu'elle illustre bien le problème du calcul de la moyenne synchrone dans le cas d'engrenages.
Nous avons défini dans ce chapitre la notion de cycloergodicité qui nous permet d'utiliser une seule réalisation de durée suffisamment longue. En pratique, nous supposons implicitement cette propriété vérifiée. Nous avons également défini les outils permettant de caractériser la cyclostationnarité et la quasi-cyclostationnarité aux ordres ![]() et
et ![]() . Enfin, un exemple montre les limites de l'approche cyclostationnaire et l'intérêt de l'approche polycyclostationnaire pour les signaux d'engrenages.
. Enfin, un exemple montre les limites de l'approche cyclostationnaire et l'intérêt de l'approche polycyclostationnaire pour les signaux d'engrenages.
Le chapitre suivant va illustrer l'utilisation de la cyclostationnarité dans le cadre de signaux pseudo-quasicyclostationnaires sur les signaux de roulement.