Dans le chapitre précédent, la cyclostationnarité a été définie. Toutes les définitions ont été introduites à l'aide de la variable angulaire ; la variable générique des machines tournantes. Néanmoins, les acquisitions dans le domaine angulaire dont nous rappellerons leur mise en ![]() uvre technique sont peu courantes. Nous proposerons donc des méthodes de re-échantillonnage en fonction de l'angle à partir des signaux à variable générique temporelle. Ces méthodes seront comparées avec l'échantillonnage angulaire direct (plus couteux et contraignant du point de vue expérimental).
uvre technique sont peu courantes. Nous proposerons donc des méthodes de re-échantillonnage en fonction de l'angle à partir des signaux à variable générique temporelle. Ces méthodes seront comparées avec l'échantillonnage angulaire direct (plus couteux et contraignant du point de vue expérimental).
Le principe d'une chaîne d'acquisition angulaire est présenté sur la figure ![]() .
.
Un codeur angulaire fixé à un arbre de la machine tournante permet d'obtenir une information de position relative. Le codeur délivre un signal carré dont la fréquence est un multiple de la fréquence de rotation. Un top tour permet d'obtenir une position de référence utile pour la localisation.
Notre chaîne d'acquisition utilise un codeur optique incrémental.
Si le codeur optique fournit un signal à une fréquence ``trop élevée'' pour l'application (![]() fronts montants/tours par exemple), il est possible de réduire cette dernière à l'aide d'un diviseur de fréquence (compteur utilisé comme diviseur par
fronts montants/tours par exemple), il est possible de réduire cette dernière à l'aide d'un diviseur de fréquence (compteur utilisé comme diviseur par ![]() ). Ce signal sera alors utilisé comme horloge externe par la carte d'acquisition. Au LASPI, nous utilisons souvent
). Ce signal sera alors utilisé comme horloge externe par la carte d'acquisition. Au LASPI, nous utilisons souvent ![]() ou
ou ![]() points/tour.
points/tour.
Comme dans toute chaîne d'acquisition classique, les signaux issus des capteurs sont conditionnés, amplifiés, puis préalablement filtrés.
La vitesse de la machine tournante peut varier au cours du temps, aussi la fréquence d'échantillonnage ainsi que la fréquence de Shanon/Nyquist varient également. Il est donc nécessaire de pouvoir changer la fréquence du filtre anti-repliement au cours de l'acquisition pour suivre ces variations de fréquence. Pour cela, il est possible d'utiliser un filtre anti-repliement à capacités commutées dont la fréquence de coupure dépend d'une fréquence externe. Sur le matériel utilisé au LASPI, cette fréquence doit être ![]() fois plus élevée que la fréquence de coupure du filtre. Un multiplicateur de fréquence est alors nécessaire.
fois plus élevée que la fréquence de coupure du filtre. Un multiplicateur de fréquence est alors nécessaire.
Pour de faibles fluctuations de vitesse, il est possible de simplifier le système. Dans ce cas, la fréquence du filtre anti-repliement est réglée pour satisfaire la condition de Nyquist correspondant à la vitesse la plus faible. On économise alors l'utilisation d'un multiplicateur de fréquence.
Un tel système (avec ou sans multiplicateur) présente des avantages importants :
Néanmoins, il présente certains inconvénients [#!potter:new!#] :
Tous ces inconvénients nous ont amenés à développer des algorithmes de re-échantillonnage a posteriori. Ces algorithmes permettent d'estimer le signal échantillonné angulairement à partir d'un signal échantillonné temporellement [#!bonnardot:use!#] en exploitant un capteur de position, voire dans certaines applications aucun capteur.
Le re-échantillonnage angulaire a posteriori ou ``order tracking'' est une alternative intéressante à l'échantillonnage angulaire direct. Il n'est plus nécessaire d'investir dans une instrumentation coûteuse, et il est possible de travailler à la fois dans le domaine angulaire et dans le domaine temporel.
Dans ce chapitre nous allons présenter une méthode générale d'échantillonnage angulaire a posteriori. Des éléments seront ensuite modifiés afin de passer en revue les divers algorithmes : du plus simple basé sur l'utilisation du signal codeur, au plus élaboré ne nécessitant pas de codeur optique.
La figure ![]() montre le principe du re-échantillonnage a posteriori :
montre le principe du re-échantillonnage a posteriori :
Outre le signal à re-échantillonner
![]() (signal accéléromètrique par exemple), un signal
(signal accéléromètrique par exemple), un signal
![]() contenant une information sur la position (le codeur optique par exemple) est nécessaire. Ces deux signaux peuvent être identiques si on estime la position à partir du signal accélèromètrique. Il est important de noter que ces signaux sont préalablement acquis temporellement.
contenant une information sur la position (le codeur optique par exemple) est nécessaire. Ces deux signaux peuvent être identiques si on estime la position à partir du signal accélèromètrique. Il est important de noter que ces signaux sont préalablement acquis temporellement.
Le but de ce paragraphe étant de décrire une méthode générale de re-échantillonnage nous considérons pour l'instant la partie estimation de position comme une boîte noire. En effet, mis à part cette partie, toutes les autres étapes sont les mêmes pour les algorithmes que nous allons présenter.
Soit ![]() la période d'échantillonage. La suite
la période d'échantillonage. La suite
![]() des positions de l'arbre correspondant aux échantillons
des positions de l'arbre correspondant aux échantillons
![]() est tout d'abord estimée à l'aide de
est tout d'abord estimée à l'aide de
![]() . Cette étape va changer selon la méthode de re-échantillonnage employée. Elle fera l'objet d'un paragraphe entier. La position estimée ou phase
. Cette étape va changer selon la méthode de re-échantillonnage employée. Elle fera l'objet d'un paragraphe entier. La position estimée ou phase
![]() (en radians) permet également de calculer la fréquence instantanée, c'est-à-dire la vitesse de l'arbre à l'aide de la relation :
(en radians) permet également de calculer la fréquence instantanée, c'est-à-dire la vitesse de l'arbre à l'aide de la relation :
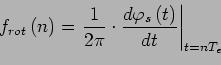 |
(2.1) |
Où la notation ![]() signifie évalué en
signifie évalué en ![]() .
.
La dérivation pouvant être approximé dans le domaine discret par des différences.
Le re-échantillonnage implique le respect des conditions de Nyquist. Malheureusement, l'intervalle de temps entre chaque échantillon n'est pas constant. Le filtre anti-repliement numérique est donc configuré selon la plus basse fréquence de rotation instantanée ainsi que le nombre d'échantillons par tour désiré après re-échantillonnage ![]() . Le plus grand intervalle de temps entre deux échantillons dans le domaine angulaire est donné par :
. Le plus grand intervalle de temps entre deux échantillons dans le domaine angulaire est donné par :
![\begin{displaymath}
\Delta n_{max}=\frac{1}{spr\cdot \min\left[f_{rot}\left(n\right)\right]} \text{ en seconde}
\end{displaymath}](img278.png) |
(2.2) |
Dès lors la fréquence de Nyquist sera :
![\begin{displaymath}
f_{Nyquist}=\frac{spr\cdot \min\left[f_{rot}\left(n\right)\right]}{2} \text{ en Hz}
\end{displaymath}](img279.png) |
(2.3) |
Il faudra prendre garde à ne pas déphaser le signal lors du filtrage en utilisant, de préférence, un filtre ![]() symétrique (en compensant le retard pur) ou un filtre du type forward-backward tel que la fonction ``filtfilt.m'' dans matlab. Le principe du filtrage forward-backward est de filtrer une première fois le signal, de le retourner, de filtrer la version retournée puis de le retourner une nouvelle fois (figure
symétrique (en compensant le retard pur) ou un filtre du type forward-backward tel que la fonction ``filtfilt.m'' dans matlab. Le principe du filtrage forward-backward est de filtrer une première fois le signal, de le retourner, de filtrer la version retournée puis de le retourner une nouvelle fois (figure ![]() ). Ce type de filtrage n'agit pas sur la phase mais élève au carré l'amplitude du filtre associé.
). Ce type de filtrage n'agit pas sur la phase mais élève au carré l'amplitude du filtre associé.
Comme la fréquence instantanée est une estimation, la fréquence de Nyquist est également une estimation. L'utilisation d'une marge de sécurité doit alors être envisagée.
En pratique, il est possible de contourner cette étape en choisissant ![]() tel que pour la fréquence d'échantillonnage
tel que pour la fréquence d'échantillonnage ![]() :
:
![]() . Dans ce cas, l'intervalle entre deux échantillons angulaires sera toujours inférieur ou égal à l'intervalle entre deux échantillons temporels et le filtrage ne sera plus nécessaire. Si les fluctuations de vitesse sont faibles, la taille des signaux re-échantillonnés est alors voisine de la taille des signaux temporels.
. Dans ce cas, l'intervalle entre deux échantillons angulaires sera toujours inférieur ou égal à l'intervalle entre deux échantillons temporels et le filtrage ne sera plus nécessaire. Si les fluctuations de vitesse sont faibles, la taille des signaux re-échantillonnés est alors voisine de la taille des signaux temporels.
A l'aide de
![]() , il est possible par interpolation, d'estimer le signal accélèrométrique pour des positions d'arbre correspondant à un incrément angulaire constant
, il est possible par interpolation, d'estimer le signal accélèrométrique pour des positions d'arbre correspondant à un incrément angulaire constant
![]() . La figure
. La figure ![]() illustre ce procédé pour un échantillon donné.
illustre ce procédé pour un échantillon donné.
Des algorithmes détaillés de diverses méthodes d'interpolation se trouvent dans [#!press:numerical!#]. Nous rappellons ci-dessous les ![]() méthodes principales :
méthodes principales :
L'interpolation de Fourier considère que le signal est à bande limitée et périodique. Ainsi, pour un signal correctement échantillonné (fréquence d'échantillonnage supérieure à deux fois la bande du signal), il est possible de reconstruire le signal pour n'importe quel instant en utilisant la formule :
![\begin{displaymath}
x\left(t\right)=\sum_{n=-\infty}^\infty x\left(n\cdot\Delta...
...\Delta_t\right]}{\pi \left(t-n\cdot \Delta_t\right)/\Delta_t}
\end{displaymath}](img286.png) |
(2.4) |
Cette interpolation bien qu'idéale, doit être adaptée comme indiqué dans [#!candocia:comments!#] car le nombre de termes est infini.
L'interpolation polynomiale est basée sur la formule de Lagrange qui utilise un polynôme d'ordre ![]() pour interpoler
pour interpoler ![]() points :
points :
 |
(2.5) |
où :
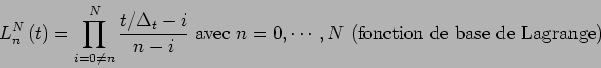 |
(2.6) |
L'interpolation de Lagrange n'impose pas de contrainte de continuité sur les dérivées. Elle pourra ainsi générer des signaux interpolés dont la dérivée présente des discontinuités, alors qu'en général, les signaux réels ont des dérivées continues. Ceci est un gros inconvénient puisque la vocation de l'interpolation est d'estimer les valeurs du signal réel et ne doit donc pas supprimer ses propriétés.
Les splines sont des morceaux de polynômes connectés ensemble ``sans à coup'' [#!unser:splines!#]. L'ordre ![]() des splines correspond à l'ordre des polynômes (par exemple, pour
des splines correspond à l'ordre des polynômes (par exemple, pour ![]() , on utilise des droites). Le lissage entre chacun des polynômes est assuré par une contrainte de continuité sur les splines et leurs dérivées jusqu'à l'ordre
, on utilise des droites). Le lissage entre chacun des polynômes est assuré par une contrainte de continuité sur les splines et leurs dérivées jusqu'à l'ordre ![]() . Des informations plus détaillées sur les splines peuvent être trouvées dans [#!unser:splines!#,#!deboor:spline!#,#!lim:online!#,#!mcfadden:interpolation!#,#!unser:bspline!#].
. Des informations plus détaillées sur les splines peuvent être trouvées dans [#!unser:splines!#,#!deboor:spline!#,#!lim:online!#,#!mcfadden:interpolation!#,#!unser:bspline!#].
Il est possible de considérer les splines comme des filtres et de calculer leur réponse impulsionnelle (figure ![]() ) et fréquentielle (
) et fréquentielle (![]() ) [#!mcfadden:interpolation!#].
) [#!mcfadden:interpolation!#].
Ces figures montrent le lien entre les splines et l'interpolation de Fourier. Pour un ordre infini, la réponse impulsionnelle des splines tend vers le sinus cardinal et la réponse fréquentielle vers le filtre passe bas idéal (cf. interpolation de Fourier dans [#!candocia:comments!#]). D'une certaine manière, les splines peuvent être considérées comme des filtres passe-bas, mais il ne faut pas perdre de vue que la fréquence de coupure de ce filtre est la fréquence de Nyquist du signal original (pour un ordre infini). Les splines sont une façon perfectionnée de relier des points comme sur du papier millimétré avec un stylo : si le signal n'est pas correctement échantillonné, les splines ne devineront pas les points manquants.
Il existe d'autres méthodes d'interpolation (fonction rationnelle, ...). Nous avons choisi d'utiliser les splines car elles imposent des contraintes de continuité, et elles se rapprochent de l'interpolation de Fourier.
Le signal re-échantillonné angulairement
![]() est obtenu à l'issue de l'interpolation. Nous allons maintenant nous intéresser à l'estimation de la position de l'arbre.
est obtenu à l'issue de l'interpolation. Nous allons maintenant nous intéresser à l'estimation de la position de l'arbre.
Des méthodes basées sur le codeur ou le top tour ont été décrites et analysées dans [#!fyfe:analysis!#] (en utilisant des signaux synthétiques). Dans [#!potter:new!#] et [#!bruel:order!#], il est possible de trouver une comparaison avec les anciennes méthodes et un exemple d'application commercial.
Ces méthodes utilisent une chaîne d'acquisition temporelle. Le signal issu, soit du codeur, soit du top tour (le plus souvent), est acquis en parallèle avec les autres signaux. Les autres étapes sont réalisées de manière logicielle.
Tout d'abord, le temps d'arrivée de l'impulsion issue du codeur est calculé en utilisant un détecteur de front montant. La méthode la plus simple consiste à détecter le passage d'un seuil. Il est possible d'améliorer la précision en prenant en compte les échantillons suivants et précédents afin de réaliser une interpolation. La figure ![]() compare ses deux approches. Le signal avant échantillonnage est en pointillé et les échantillons sont représentés par des ronds. Cette figure montre clairement l'apport de l'interpolation. Il est nécessaire d'utiliser une fréquence d'échantillonnage élevée vis à vis de la bande passante des signaux mécaniques pour détecter avec précision l'instant de franchissement du seuil. On sur-échantillonne donc les autres signaux (seules quelques cartes d'acquisitions permettent d'utiliser des fréquences d'échantillonnage différentes pour certains canaux).
compare ses deux approches. Le signal avant échantillonnage est en pointillé et les échantillons sont représentés par des ronds. Cette figure montre clairement l'apport de l'interpolation. Il est nécessaire d'utiliser une fréquence d'échantillonnage élevée vis à vis de la bande passante des signaux mécaniques pour détecter avec précision l'instant de franchissement du seuil. On sur-échantillonne donc les autres signaux (seules quelques cartes d'acquisitions permettent d'utiliser des fréquences d'échantillonnage différentes pour certains canaux).
Une fois les impulsions détectées, la position de l'arbre est estimée. Soit le nombre d'impulsions par tour ![]() fourni par le codeur (
fourni par le codeur (![]() dans le cas d'un top tour). Chaque instant détecté correspond à un incrément angulaire de
dans le cas d'un top tour). Chaque instant détecté correspond à un incrément angulaire de
![]() . Dans [#!fyfe:analysis!#], l'interpolation est faite à l'aide d'un polynôme d'ordre
. Dans [#!fyfe:analysis!#], l'interpolation est faite à l'aide d'un polynôme d'ordre ![]() :
:
La résolution de cette équation fournit la position ou phase en fonction du temps et donc
![]() aux instants d'échantillonnage. Cette méthode d'interpolation pourra être remplacée par des splines lorsque l'on n'a pas de contrainte de temps réel. Il est alors ensuite possible d'utiliser l'algorithme général d'échantillonnage a posteriori.
aux instants d'échantillonnage. Cette méthode d'interpolation pourra être remplacée par des splines lorsque l'on n'a pas de contrainte de temps réel. Il est alors ensuite possible d'utiliser l'algorithme général d'échantillonnage a posteriori.
Bien que l'interpolation où l'équation ![]() soit capable de fournir la phase à n'importe quel instant, la précision est limitée par le nombre de points par tour. En effet, si le signal tachymétrique est un top tour, on ne pourra pas obtenir une précision supérieure au tour. La vitesse estimée à l'intérieur du tour sera donc une vitesse moyenne lissée. Il conviendra donc de déterminer le nombre de points par tour selon la finesse de l'analyse choisie ou des contraintes matérielles. Un re-échantillonnage au top tour permettra d'obtenir des signaux avec un nombre constant de points par tour, mais ne compensera pas les variations de vitesse à l'intérieur du tour. Dès lors, ces variations de vitesse non compensées se retrouveront dans la contribution résiduelle (c'est-à-dire non périodique du signal). Nous étudierons la différence entre les signaux top tour et codeur optique plus loin. Fort heureusement les fluctuations de vitesse restent faibles (quelques pour mille voire quelques pour cent), dès lors, la contribution résiduelle engendrée sera de faible énergie. Néanmoins, cette erreur deviendra de plus en plus préjudiciable pour des méthodes de diagnostic travaillant en ``hautes fréquences'' (relativement au signal tachymétrique) puisque la reconstruction sera basée sur un signal basse fréquence dans le cas d'un top tour. Dans [#!fyfe:analysis!#], il est conclu qu'en théorie l'augmentation du nombre de points par tour doit apporter une amélioration. Néanmoins, il n'a été trouvé aucun test pour étayer cet argument. Cela s'explique notamment par l'inertie de la machine qui limite les fluctuations de vitesse haute fréquence, en agissant comme un filtre passe bas. Cette limitation réduit le nombre de points par tour minimal nécessaire pour obtenir de ``bons résultats''.
soit capable de fournir la phase à n'importe quel instant, la précision est limitée par le nombre de points par tour. En effet, si le signal tachymétrique est un top tour, on ne pourra pas obtenir une précision supérieure au tour. La vitesse estimée à l'intérieur du tour sera donc une vitesse moyenne lissée. Il conviendra donc de déterminer le nombre de points par tour selon la finesse de l'analyse choisie ou des contraintes matérielles. Un re-échantillonnage au top tour permettra d'obtenir des signaux avec un nombre constant de points par tour, mais ne compensera pas les variations de vitesse à l'intérieur du tour. Dès lors, ces variations de vitesse non compensées se retrouveront dans la contribution résiduelle (c'est-à-dire non périodique du signal). Nous étudierons la différence entre les signaux top tour et codeur optique plus loin. Fort heureusement les fluctuations de vitesse restent faibles (quelques pour mille voire quelques pour cent), dès lors, la contribution résiduelle engendrée sera de faible énergie. Néanmoins, cette erreur deviendra de plus en plus préjudiciable pour des méthodes de diagnostic travaillant en ``hautes fréquences'' (relativement au signal tachymétrique) puisque la reconstruction sera basée sur un signal basse fréquence dans le cas d'un top tour. Dans [#!fyfe:analysis!#], il est conclu qu'en théorie l'augmentation du nombre de points par tour doit apporter une amélioration. Néanmoins, il n'a été trouvé aucun test pour étayer cet argument. Cela s'explique notamment par l'inertie de la machine qui limite les fluctuations de vitesse haute fréquence, en agissant comme un filtre passe bas. Cette limitation réduit le nombre de points par tour minimal nécessaire pour obtenir de ``bons résultats''.
Une méthode hybride a été proposée dans [#!bossley:hybrid!#] : K.M. Bossley propose d'adjoindre à la carte d'acquisition un compteur rapide (c'est-à-dire un trigger analogique). La détection du top tour n'étant plus faite de manière logicielle mais matérielle, il n'est donc plus nécessaire de sur-échantillonner le signal. De plus, comme les mesures sont faites de manière externe elles sont plus précises.
Une implantation temps réel de cette méthode peut être trouvée dans [#!crapart:implantation!#].
Ces techniques ne nécessitent plus de chaîne d'acquisition angulaire mais imposent encore l'utilisation d'un codeur. C'est pourquoi nous proposons de nouvelles méthodes exploitant l'information contenue dans le signal accéléromètrique [#!bonnardot:use!#] et [#!bonnardot:reechantillonnage!#]. Les méthodes suivantes ont été développées pour des signaux d'engrenages.
Cette méthode repose sur l'utilisation du signal accéléromètrique (moyennant certaines contraintes notamment sur les variations de vitesse). La fréquence d'engrènement résultant des contacts entre les dents est utilisée afin de déterminer la position de l'arbre.
Le modèle présenté par McFadden dans [#!mcfadden:detecting!#] et plus récemment dans [#!wang:early!#] est utilisé :
Où :

Les fonctions
![]() et
et
![]() sont induites par la rotation des deux roues et comportent également des informations sur leurs imperfections (dans le modèle original, elles étaient utilisées pour représenter un défaut local d'une dent). Dès lors,
sont induites par la rotation des deux roues et comportent également des informations sur leurs imperfections (dans le modèle original, elles étaient utilisées pour représenter un défaut local d'une dent). Dès lors, ![]() est composée de deux signaux périodiques selon la période de rotation de la roue menante et de la roue menée (
est composée de deux signaux périodiques selon la période de rotation de la roue menante et de la roue menée (![]() et
et ![]() ). Plus de détails concernant les signaux vibratoires sont répertoriés dans [#!randall:new!#] et [#!elbadaoui:modelling!#].
). Plus de détails concernant les signaux vibratoires sont répertoriés dans [#!randall:new!#] et [#!elbadaoui:modelling!#].
La figure ![]() montre le spectre d'un tel signal sans fluctuation de vitesse (banc d'essais du LASPI). Il est composé :
montre le spectre d'un tel signal sans fluctuation de vitesse (banc d'essais du LASPI). Il est composé :
![]() est ensuite convolué avec la réponse de la structure mécanique.
est ensuite convolué avec la réponse de la structure mécanique.
D'après le modèle, la fréquence de l'arbre ![]() et donc sa position (ou phase) est contenue dans la version temporelle du signal. Il sera alors exploité afin d'estimer la position de l'arbre en vue de faire du re-échantillonnage angulaire.
et donc sa position (ou phase) est contenue dans la version temporelle du signal. Il sera alors exploité afin d'estimer la position de l'arbre en vue de faire du re-échantillonnage angulaire.
Afin de prendre en compte les fluctuations de vitesse, il est nécessaire de remplacer ![]() par
par
![]() dans
dans ![]() . Chaque fréquence notée sans
. Chaque fréquence notée sans
![]() sera maintenant considérée comme une fréquence moyenne. La modulation de phase
sera maintenant considérée comme une fréquence moyenne. La modulation de phase
![]() sera alors interprétée comme une fluctuation de vitesse et sera incluse dans
sera alors interprétée comme une fluctuation de vitesse et sera incluse dans
![]() . Nous ne nous intéressons pas ici au système de type broyeur de pierres où la vitesse est fortement liée aux pierres concassées c'est-à-dire à la charge. Nous considérons également que le régime est établi. Le modèle devient alors :
. Nous ne nous intéressons pas ici au système de type broyeur de pierres où la vitesse est fortement liée aux pierres concassées c'est-à-dire à la charge. Nous considérons également que le régime est établi. Le modèle devient alors :
Un filtre passe bande centré sur la fréquence d'engrènement (ou une de ses harmoniques)
![]() et excluant les bandes latérales et autres perturbations permet d'isoler la fréquence d'engrènement (ou une de ses harmoniques). Le réglage de la bande passante doit être réalisé en observant le spectre avec une bonne résolution fréquentielle.
et excluant les bandes latérales et autres perturbations permet d'isoler la fréquence d'engrènement (ou une de ses harmoniques). Le réglage de la bande passante doit être réalisé en observant le spectre avec une bonne résolution fréquentielle.
Comme la vitesse fluctue avec le temps, les pics sont remplacés par une distribution autour de la fréquence moyenne, des ``collisions'' sont alors possibles entre les harmoniques et les bandes latérales dans le spectre (cf. figure ![]() pour un cas extrême issu du banc d'essais du LIS avant changement des engrenages). Si les variations de vitesse sont trop importantes, le motif associé à la fréquence d'engrènement va recouvrir les bandes latérales rendant impossible l'estimation à l'aide de notre méthode. En effet, après le filtrage passe bas, deux fréquences seront présentes au lieu d'une.
pour un cas extrême issu du banc d'essais du LIS avant changement des engrenages). Si les variations de vitesse sont trop importantes, le motif associé à la fréquence d'engrènement va recouvrir les bandes latérales rendant impossible l'estimation à l'aide de notre méthode. En effet, après le filtrage passe bas, deux fréquences seront présentes au lieu d'une.
Afin d'étudier l'effet de la variation de vitesse sur le filtre, nous allons considérer une variation de fréquence maximale ![]() . Dans un contexte stochastique, il peut être délicat de parler de maximum. Dès lors, nous pourrons, au lieu d'utiliser le maximum, caractériser cette variation en mesurant son écart type. Par exemple, dans le cas gaussien, interpréter
. Dans un contexte stochastique, il peut être délicat de parler de maximum. Dès lors, nous pourrons, au lieu d'utiliser le maximum, caractériser cette variation en mesurant son écart type. Par exemple, dans le cas gaussien, interpréter ![]() comme deux fois l'écart-type de la fluctuation de vitesse, permettrait de prendre en compte
comme deux fois l'écart-type de la fluctuation de vitesse, permettrait de prendre en compte ![]() de la distribution de la vitesse.
de la distribution de la vitesse.
Soit ![]() , le nombre maximal de dents des deux roues (menantes et menées),
, le nombre maximal de dents des deux roues (menantes et menées), ![]() la vitesse minimale moyenne, et,
la vitesse minimale moyenne, et, ![]() l'harmonique de
l'harmonique de ![]() utilisée. La fluctuation maximale de vitesse qui ne cause pas de recouvrement est :
utilisée. La fluctuation maximale de vitesse qui ne cause pas de recouvrement est :
Par exemple, pour ![]() , si la fréquence de rotation de l'arbre est de
, si la fréquence de rotation de l'arbre est de ![]() , si la seconde roue à
, si la seconde roue à ![]() dents (
dents (![]() étage de l'engrenage du LASPI), la fluctuation de vitesse maximale pour l'arbre d'entrée sera de
étage de l'engrenage du LASPI), la fluctuation de vitesse maximale pour l'arbre d'entrée sera de ![]() ou
ou ![]() de
de ![]() . Plus l'harmonique est élevée, plus la bande deviendra étroite. Cet exemple montre l'inconvénient majeur de cette méthode : elle impose une fluctuation de vitesse faible. Si cette contrainte est respectée, le filtre va extraire exclusivement et en totalité l'harmonique d'engrènement choisie. Il est important de préciser que la fréquence des variations de vitesse obtenue ne peut excéder la demi-largeur de bande qui est inférieure à la fréquence de rotation la plus basse (si l'on respecte la condition
. Plus l'harmonique est élevée, plus la bande deviendra étroite. Cet exemple montre l'inconvénient majeur de cette méthode : elle impose une fluctuation de vitesse faible. Si cette contrainte est respectée, le filtre va extraire exclusivement et en totalité l'harmonique d'engrènement choisie. Il est important de préciser que la fréquence des variations de vitesse obtenue ne peut excéder la demi-largeur de bande qui est inférieure à la fréquence de rotation la plus basse (si l'on respecte la condition ![]() ). En conséquence, les variations de vitesse à l'intérieur du tour sont invisibles : les possibilités de re-échantillonnage par cette méthode sont équivalentes au top tour.
). En conséquence, les variations de vitesse à l'intérieur du tour sont invisibles : les possibilités de re-échantillonnage par cette méthode sont équivalentes au top tour.
Si la fluctuation de vitesse est trop importante, nous aurons une version erronnée de la variation de vitesse au lieu de
![]() .
.
L'extraction de la phase instantanée ou position de l'arbre est réalisée grâce au signal analytique :
Son utilisation n'est valide que si le signal ne contient qu'une composante fréquentielle comme exigé précédemment (voir [#!boashash:estimating!#] pour plus d'information). La phase déballée (c'est-à-dire dans ![]() et non
et non
![]() ) est ensuite extraite de ce signal (complexe) :
) est ensuite extraite de ce signal (complexe) :
La position angulaire de l'arbre de l'engrenage est obtenue en divisant cette phase par le nombre de dents ainsi que par le rang de l'harmonique utilisée :
La connaissance de la cinématique de l'engrenage (nombre de dents de chaque roue) est nécessaire pour calculer la fréquence d'engrènement, mais ce n'est pas un inconvénient car sa connaissance est en générale requise pour faire du diagnostic.
Le modèle d'engrènement présenté dans (![]() ) et sa version filtrée (
) et sa version filtrée (![]() ) ne font pas apparaître de bruit. On suppose donc implicitement que ce dernier est négligeable. Nous allons maintenant étudier l'influence du bruit en faisant quelques hypothèses. Le signal après filtrage sera modèlisé par :
) ne font pas apparaître de bruit. On suppose donc implicitement que ce dernier est négligeable. Nous allons maintenant étudier l'influence du bruit en faisant quelques hypothèses. Le signal après filtrage sera modèlisé par :
| (2.15) |
Où le deuxième terme
![]() représente le bruit. Ce terme pourra être écrit sous la forme
représente le bruit. Ce terme pourra être écrit sous la forme
![]() sans aucune restriction sur la phase
sans aucune restriction sur la phase
![]() . On pourra donc interpréter
. On pourra donc interpréter ![]() géométriquement comme une somme de deux vecteurs. Afin de pouvoir définir un rapport signal à bruit, nous nous placerons dans le pire des cas, c'est-à-dire
géométriquement comme une somme de deux vecteurs. Afin de pouvoir définir un rapport signal à bruit, nous nous placerons dans le pire des cas, c'est-à-dire
![]() où
où ![]() est l'amplitude maximale. Le rapport signal à bruit
est l'amplitude maximale. Le rapport signal à bruit ![]() sera alors défini par :
sera alors défini par :
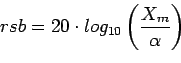 |
(2.16) |
La figure ![]() représente graphiquement
représente graphiquement
![]() pour un échantillon
pour un échantillon ![]() donné. Il existe deux cas.
donné. Il existe deux cas.
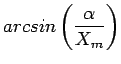 |
(2.17) | ||
| (2.18) |
La figure ![]() montre l'erreur de phase maximale commise en fonction du rapport signal sur bruit. Elle est très sensible au bruit puisque pour
montre l'erreur de phase maximale commise en fonction du rapport signal sur bruit. Elle est très sensible au bruit puisque pour ![]() , l'erreur est de
, l'erreur est de ![]() . Néanmoins, il ne faut pas perdre de vue que la phase est estimée à partir d'une fréquence d'engrènement. Dès lors, cette erreur est divisée, d'une part par le rang de l'harmonique et d'autre part par le nombre de dents de l'arbre, soit une précision de
. Néanmoins, il ne faut pas perdre de vue que la phase est estimée à partir d'une fréquence d'engrènement. Dès lors, cette erreur est divisée, d'une part par le rang de l'harmonique et d'autre part par le nombre de dents de l'arbre, soit une précision de
![]() sur notre banc d'essai si on se base sur l'harmonique
sur notre banc d'essai si on se base sur l'harmonique
![]() .
.
L'estimation de position basée sur la démodulation autour de la fréquence d'engrènement exploite un modèle de signal d'engrenages mais ne prend pas en compte l'aspect cyclostationnaire. En observant les signaux accéléromètriques issus d'engrenages, l'idée de recaler (ou synchroniser) les cycles les uns par rapport aux autres afin de réduire les fluctuations de vitesse nous est apparue de manière assez intuitive. Le paragraphe suivant présente cette méthode.
Les signaux vibratoires d'engrenage sont cyclostationnaires dans le domaine angulaire. La contribution cyclostationnaire à l'ordre ![]() (périodique) représentant une part importante de l'énergie du signal, nous avons eu l'idée de tirer parti des similitudes d'aspect entre les cycles.
(périodique) représentant une part importante de l'énergie du signal, nous avons eu l'idée de tirer parti des similitudes d'aspect entre les cycles.
Le champ d'application de cette méthode est beaucoup plus étendu que la méthode précédente limitée aux engrenages : cette méthode est valable pour tous signaux présentant une composante cyclostationnaire à l'ordre ![]() (similitudes).
(similitudes).
Un engrenage contenant plusieurs étages possède plusieurs périodes cycliques ![]() dans un rapport rationnel entre elles. Chacune d'elle est un diviseur d'une période commune
dans un rapport rationnel entre elles. Chacune d'elle est un diviseur d'une période commune ![]() . Pour faire apparaître les similitudes, le signal accéléromètrique sera modélisé par la somme de contributions périodiques provenant de chacune des roues de périodes
. Pour faire apparaître les similitudes, le signal accéléromètrique sera modélisé par la somme de contributions périodiques provenant de chacune des roues de périodes
![]() . Les interactions entre chacune des roues, les contributions des autres composantes mécaniques et le bruit seront contenus dans un terme
. Les interactions entre chacune des roues, les contributions des autres composantes mécaniques et le bruit seront contenus dans un terme
![]() . On pourra alors utiliser l'approximation suivante :
. On pourra alors utiliser l'approximation suivante :
Où
![]() est un peigne de Dirac convolué au signal
est un peigne de Dirac convolué au signal
![]() émis pendant un tour de la
émis pendant un tour de la
![]() roue. Il est alors possible d'interpréter chaque période comme un écho de la première. C'est pourquoi nous proposons d'utiliser un détecteur d'échos tel que le cepstre [#!bonnardot:reechantillonnage!#].
roue. Il est alors possible d'interpréter chaque période comme un écho de la première. C'est pourquoi nous proposons d'utiliser un détecteur d'échos tel que le cepstre [#!bonnardot:reechantillonnage!#].
Afin de pouvoir décrire la méthode de re-échantillonnage, nous allons tout d'abord introduire le cepstre et présenter quelques unes de ses propriétés de manière rapide.
L'efficacité du cepstre pour l'analyse vibratoire des machines tournantes a été démontrée par R.B. Randall en 1975 dans [#!randall:gearbox!#] et plus récemment dans [#!elbadaoui:new!#].
Le cepstre a été introduit par Bogert afin de détecter des échos. Il a été défini par :
La variable ![]() dans
dans
![]() n'est plus appelée temps mais quéfrence.
n'est plus appelée temps mais quéfrence.
Ce paragraphe liste les propriétés du cepstre, leurs démonstrations sont faites notamment dans [#!elbadaoui:contribution!#].
| (2.21) | |||
| (2.22) |
Un signal
![]() entaché d'écho (décalage) peut être modèlisé par :
entaché d'écho (décalage) peut être modèlisé par :
| (2.23) | |||
| (2.24) |
Un tel signal a pour cepstre :
| (2.25) |
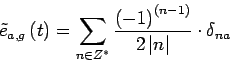 |
(2.26) |
La figure ![]() montre le cepstre d'un tel signal. Comme on peut le constater sur la figure,
montre le cepstre d'un tel signal. Comme on peut le constater sur la figure,
![]() est fortement décroissant et confiné à l'origine. La présence du peigne alterné
est fortement décroissant et confiné à l'origine. La présence du peigne alterné
![]() , fait du cepstre un outil très intéressant pour la détection d'échos.
, fait du cepstre un outil très intéressant pour la détection d'échos.
Par ailleurs, on comprend bien qu'une sinusoïde ajoutée à sa version décalée reste une sinusoïde et que le cepstre sera donc incapable d'y voir un écho.
Il est possible de généraliser la modèlisation précédente afin d'introduire l'écho multiple noté :
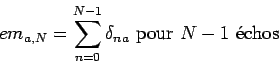 |
(2.27) |
Un signal ![]() entaché d'échos multiples peut alors être modélisé par :
entaché d'échos multiples peut alors être modélisé par :
| (2.28) |
Dans ce cas son cepstre est :
| (2.29) |
 |
(2.30) |
C'est-à-dire un peigne positif décroissant au pas ![]() plus un peigne négatif décroissant au pas
plus un peigne négatif décroissant au pas ![]() . La taille des signaux étant de l'ordre de
. La taille des signaux étant de l'ordre de ![]() , le peigne négatif est entièrement replié, donc, inexploitable.
, le peigne négatif est entièrement replié, donc, inexploitable.
Lorsque le signal contient ![]() termes d'échos multiples, son cepstre contient
termes d'échos multiples, son cepstre contient ![]() peignes positifs décroissants au pas correspondant (figure
peignes positifs décroissants au pas correspondant (figure ![]() ). La somme des premiers pics des
). La somme des premiers pics des ![]() peignes est égale à
peignes est égale à ![]() et la distribution des amplitudes est celle de la racine carrée de l'énergie des motifs auxquels chaque peigne est convolué.
et la distribution des amplitudes est celle de la racine carrée de l'énergie des motifs auxquels chaque peigne est convolué.
Le bruit diminue l'amplitude des diracs. L'amplitude du premier pic de
![]() ou
ou
![]() est de 0.5 dans le cas non bruité. Dans le cas bruité, cette valeur est multipliée par
est de 0.5 dans le cas non bruité. Dans le cas bruité, cette valeur est multipliée par ![]() où
où ![]() est l'écart type du bruit supposé blanc [#!elbadaoui:contribution!#]. Ainsi, plus le signal sera bruité, plus les diracs seront noyés dans le bruit de fond du cepstre, et plus leur détection sera ardue.
est l'écart type du bruit supposé blanc [#!elbadaoui:contribution!#]. Ainsi, plus le signal sera bruité, plus les diracs seront noyés dans le bruit de fond du cepstre, et plus leur détection sera ardue.
Si le décalage est distribué autour d'un décalage moyen a, le terme d'écho est noté :
| (2.31) |
où g représente cette distribution. Alors, il admet comme cepstre [#!fournel:utilisation!#] :
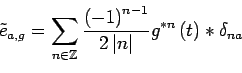 |
(2.32) |
Où
![]() correspond à
correspond à
![]() convolué
convolué ![]() fois avec lui même.
fois avec lui même.
Dans un écho multiple, si les pics du cepstre sont distribués, le premier pic du cepstre reproduit cette distribution.
Tout l'intérêt du cepstre réside dans l'homomorphisme : les motifs périodiques ainsi que la réponse impulsionnelle de la structure contenus dans
![]() se trouveront surtout au début du cepstre (leur contribution décroît assez vite), et seront nettement différenciés des diracs associés à la périodicité. La figure
se trouveront surtout au début du cepstre (leur contribution décroît assez vite), et seront nettement différenciés des diracs associés à la périodicité. La figure ![]() montre les premiers points du cepstre d'un signal d'engrenage. On distingue clairement les pics associés à l'arbre d'entrée
montre les premiers points du cepstre d'un signal d'engrenage. On distingue clairement les pics associés à l'arbre d'entrée ![]() et à l'arbre de sortie
et à l'arbre de sortie ![]() .
.
L'emploi du cepstre, sur des signaux temporels avec des fluctuations de vitesse, contraint à se limiter à un écho, c'est-à-dire, deux tours de l'arbre étudié. En effet, utiliser plus de tours contribuerait d'une part à remplacer les diracs par une distribution dispersant l'énergie et d'autre part, fournirait une position moyennée sur plusieurs tours alors que l'on veut estimer une position instantanée. L'utilisation du cepstre sur ![]() tours permet en théorie d'obtenir l'équivalent d'un top tour puisque la position est estimée pour chaque tour.
tours permet en théorie d'obtenir l'équivalent d'un top tour puisque la position est estimée pour chaque tour.
A priori, le cepstre pourrait être calculé sur une fenêtre glissante afin d'estimer le ``décalage'' entre le
![]() tour et le
tour et le
![]() tour. Un calcul par intégration permettant d'en déduire la phase. Néanmoins, l'intégration produirait une accumulation des imprécisions de positions locales et serait préjudiciable au re-échantillonnage. C'est pourquoi nous allons prendre le signal accéléromètrique du premier tour comme référence et le comparer successivement aux autres tours.
tour. Un calcul par intégration permettant d'en déduire la phase. Néanmoins, l'intégration produirait une accumulation des imprécisions de positions locales et serait préjudiciable au re-échantillonnage. C'est pourquoi nous allons prendre le signal accéléromètrique du premier tour comme référence et le comparer successivement aux autres tours.
La méthode est présentée sur la figure ![]() . Cette méthode nécessite la connaissance de la période approximative de rotation de l'arbre d'entrée
. Cette méthode nécessite la connaissance de la période approximative de rotation de l'arbre d'entrée ![]() obtenue en calculant le cepstre sur tout le signal (
obtenue en calculant le cepstre sur tout le signal (![]() est alors le centre de gravité du
est alors le centre de gravité du ![]() pic du cepstre).
pic du cepstre).
![\begin{displaymath}
\hat{\varphi_s}\left[T_1\left(i-1\right)\right]=\left(i-1-\frac{\hat{p}_i}{T_1}\right)\cdot 2 \pi
\end{displaymath}](img409.png) |
(2.33) |
On utilisera ensuite l'algorithme général de re-échantillonnage a posteriori pour obtenir le signal dans le domaine angulaire.
Comme ce sont des décalages entre tours qui sont utilisés, l'estimation de position est équivalente à un top tour.
L'atout majeur du cesptre par rapport à l'autocorrélation est de simplifier la détection des décalages grâce à des pics très étroits, néanmoins, il reste sensible au bruit. La corrélation quant à elle concentre le bruit au retard ![]() mais est également un outil réputé pour la détection de retard. Le retard est matérialisé par le maximum d'un motif large ce qui entraine une estimation moins précise des retards.
mais est également un outil réputé pour la détection de retard. Le retard est matérialisé par le maximum d'un motif large ce qui entraine une estimation moins précise des retards.
La robustesse de la corrélation vis à vis du bruit a été combinée aux performances du cepstre pour créer le cepstre robuste présenté dans [#!antoni:some!#]. Le cepstre robuste
![]() est défini par :
est défini par :
| (2.34) |
Il suffira de remplacer le cepstre classique par le cepstre robuste dans l'algorithme précédent pour augmenter la robustesse vis à vis du bruit. Le cepstre robuste ralentit les calculs puisqu'il nécessite le calcul d'une corrélation. Néanmoins, en présence de bruit, il devient incontournable.
Ce chapitre montre pas à pas comment utiliser les méthodes de re-échantillonnage basées sur le signal.
Les signaux proviennent du banc d'essai du LASPI. Ce dernier est constitué de deux réducteurs montés dans une configuration ``back to back'' (voir figure ![]() ).
).
Pour charger une machine tournante, il est courant d'utiliser un autre moteur configuré en générateur. L'énergie électrique est alors dissipée dans des résistances ou est absorbée par le réseau électrique.
Malheureusement, notre réducteur a un rapport de réduction assez élevé : 140. Dès lors, le couple en sortie du réducteur est ![]() fois plus grand que le couple d'entrée. Le moteur électrique nécessaire à la charge de notre réducteur serait d'une part gigantesque et d'autre part fort coûteux. Aussi nous utilisons une solution mécanique de type back to back plutôt qu'une solution électrique.
fois plus grand que le couple d'entrée. Le moteur électrique nécessaire à la charge de notre réducteur serait d'une part gigantesque et d'autre part fort coûteux. Aussi nous utilisons une solution mécanique de type back to back plutôt qu'une solution électrique.
Cette technique nécessite de posséder deux réducteurs identiques. Les deux arbres de sortie (petite vitesse - fort couple) sont reliés. Les deux arbres d'entrée (grande vitesse - faible couple) sont également connectés mais avec l'application préalable d'un couple entre ces derniers. Le couple appliqué sur l'arbre petite vitesse est multiplié par ![]() sur l'arbre grande vitesse, ce qui peut correspondre à une très forte charge. Le moteur fournit juste l'énergie nécessaire pour faire tourner l'engrenage, et compenser les pertes mécaniques.
sur l'arbre grande vitesse, ce qui peut correspondre à une très forte charge. Le moteur fournit juste l'énergie nécessaire pour faire tourner l'engrenage, et compenser les pertes mécaniques.
Le nombre de dents associé à chacune des roues est indiqué sur le schéma. Le moteur est alimenté directement sans utilisation de variateur. Un couplemètre positionné sur l'arbre commun d'entrée indique la charge différentielle appliquée. Les réducteurs produits par la société FOC Transmissions (Vienne) référence APA 4T 24 6H 2B sont des réducteurs de la série ATLAS à 4 trains parallèles capables de transmettre une puissance mécanique de ![]() pour une vitesse d'entrée de
pour une vitesse d'entrée de ![]() , soit un couple maximum de
, soit un couple maximum de ![]() en entrée et de
en entrée et de ![]() en sortie.
en sortie.
Un codeur optique est placé sur l'arbre d'entrée, il permettra d'évaluer les algorithmes d'échantillonnage a posteriori. Les signaux ont été acquis avec une carte d'acquisition ![]() (soit une dynamique de
(soit une dynamique de ![]() ), une fréquence d'échantillonnage
), une fréquence d'échantillonnage ![]() , un filtre passe bas de fréquence de coupure
, un filtre passe bas de fréquence de coupure ![]() . Un million de points ont été enregistrés avec une charge de
. Un million de points ont été enregistrés avec une charge de ![]() en entrée du réducteur. Les figures
en entrée du réducteur. Les figures ![]() et
et ![]() donnent un aperçu rapide du signal vibratoire. Le maximum du spectre se trouve à
donnent un aperçu rapide du signal vibratoire. Le maximum du spectre se trouve à ![]() et il y a une perte de
et il y a une perte de ![]() dûe à l'ajustage des gains. Dès lors, le niveau significatif le plus bas est de
dûe à l'ajustage des gains. Dès lors, le niveau significatif le plus bas est de
![]() . La partie droite du spectre est en dessous de ce niveau. Les pics entre
. La partie droite du spectre est en dessous de ce niveau. Les pics entre ![]() et
et ![]() sont probablement causés par l'électronique présente dans le filtre anti-repliement à capacités commutées. Ce spectre est juste un aperçu (faible résolution fréquentielle - fort moyennage) et ne fait donc pas apparaître les fréquences d'engrènement et de rotation qui nécessiteraient d'une part une meilleure résolution fréquentielle et d'autre part une observation sur une bande de fréquence limitée.
sont probablement causés par l'électronique présente dans le filtre anti-repliement à capacités commutées. Ce spectre est juste un aperçu (faible résolution fréquentielle - fort moyennage) et ne fait donc pas apparaître les fréquences d'engrènement et de rotation qui nécessiteraient d'une part une meilleure résolution fréquentielle et d'autre part une observation sur une bande de fréquence limitée.
La majeure partie de la puissance est contenue approximativement dans la bande de fréquence
![]() . Cette dernière est cohérente avec la caractéristique fréquentielle de l'accéléromètre
. Cette dernière est cohérente avec la caractéristique fréquentielle de l'accéléromètre ![]() (courbe n°4) et de sa fixation de type aimant. La fréquence d'échantillonnage n'est donc pas imposée par les signaux accéléromètriques mais par les signaux du codeur acquis en parallèle (
(courbe n°4) et de sa fixation de type aimant. La fréquence d'échantillonnage n'est donc pas imposée par les signaux accéléromètriques mais par les signaux du codeur acquis en parallèle (
![]() - fondamental à environ
- fondamental à environ ![]() ). Une période du codeur correspond, environ à 8 échantillons. Cet exemple montre la nécessité du sur-échantillonnage lors de l'acquisition simultanée de signaux issus du codeur.
). Une période du codeur correspond, environ à 8 échantillons. Cet exemple montre la nécessité du sur-échantillonnage lors de l'acquisition simultanée de signaux issus du codeur.
Comme les filtres passe-bande sont centrés sur la fréquence d'engrènement ou ses harmoniques, il sera nécessaire de déterminer avec précision la fréquence de rotation. Dans le cas contraire, l'observation du spectre permettra d'obtenir une meilleure précision en confrontant les positions approximatives des fréquences d'engrènement (harmoniques incluses) et des bandes latérales aux positions des ``pics'' dans le spectre. Cette étape peut être réalisée en plaçant des curseurs sur le spectre correspondant aux positions théoriques des ``pics'' et en ajustant la position des curseurs jusqu'à la correspondance. Lors de cette étape la résolution fréquentielle du spectre doit être privilégiée.
Soit ![]() la plus grande fréquence de rotation de l'arbre étudié. Une fois cette fréquence déterminée avec précision, le spectre sera affiché dans l'intervalle
la plus grande fréquence de rotation de l'arbre étudié. Une fois cette fréquence déterminée avec précision, le spectre sera affiché dans l'intervalle
![]() afin de choisir la bande passante du filtre. Le but du filtre est de conserver uniquement la fréquence d'engrènement ou son harmonique et surtout de supprimer les fréquences parasites telle que dans la figure
afin de choisir la bande passante du filtre. Le but du filtre est de conserver uniquement la fréquence d'engrènement ou son harmonique et surtout de supprimer les fréquences parasites telle que dans la figure ![]() . Une représentation linéaire du spectre permet un choix plus facile des fréquences. Son utilisation n'exclut pas le contrôle à l'aide d'une échelle logarithmique. Comme seule la phase et non l'amplitude est utilisée, le filtre n'a aucune contrainte sur son module mais doit préserver la phase du signal. N'ayant pas de contrainte sur le module, nous avons utilisé un filtrage à l'aide d'une fenêtre rectangulaire dans le domaine fréquentiel.
. Une représentation linéaire du spectre permet un choix plus facile des fréquences. Son utilisation n'exclut pas le contrôle à l'aide d'une échelle logarithmique. Comme seule la phase et non l'amplitude est utilisée, le filtre n'a aucune contrainte sur son module mais doit préserver la phase du signal. N'ayant pas de contrainte sur le module, nous avons utilisé un filtrage à l'aide d'une fenêtre rectangulaire dans le domaine fréquentiel.
Il est nécessaire d'exploiter plusieurs harmoniques de la fréquence d'engrènement (c'est-à-dire plusieurs filtres), en effet, le modèle restant théorique, certaines harmoniques peuvent être perturbées par du bruit les rendant inexploitables. Afin de choisir parmi toutes les phases instantanées candidates, nous proposons de comparer les vitesses instantanées.
Comme le signal est ``sur-échantillonné'', il contient beaucoup d'harmoniques de la fréquence d'engrènement. Aussi, ![]() harmoniques ont été exploitées pour créer
harmoniques ont été exploitées pour créer ![]() filtres distincts. Les fréquences instantanées (ou vitesses instantanées) ont été classées en 4 groupes :
filtres distincts. Les fréquences instantanées (ou vitesses instantanées) ont été classées en 4 groupes :
Ces courbes correspondent à un premier réglage des filtres. Il est possible en réajustant certaines fréquences d'améliorer quelques résultats. Afin de montrer les résultats tels qu'ils apparaissent lors des premiers essais, nous n'avons pas fait ces ajustements. Nous avons alors pu critiquer ces courbes et mettre en évidence la nécessité d'un tel réajustement notamment pour la catégorie ``vitesses fausses''.
Ces figures montrent qu'il est important de tester autant d'harmoniques que possible afin de pouvoir faire une ``classification''. Dans cet exemple, il a été possible de tester beaucoup d'harmoniques, néanmoins sur des signaux non ``sur-échantillonnés'' le nombre de candidats sera plus faible. En cas de doute, ou si le nombre d'harmoniques est faible, il suffit d'estimer le signal dans le domaine angulaire pour chacun des candidats. Un spectre ou une moyenne synchronne permet alors de choisir le meilleur :
Une fois l'harmonique choisie, il est possible d'estimer les signaux dans le domaine angulaire. Les amplitudes des signaux re-échantillonnés suivant le premier groupe sont proches.
L'estimation fait intervenir une interpolation. En théorie, l'interpolation est capable de fournir n'importe quelle précision (nombre d'échantillons par tour). En pratique, cette dernière est limitée pour plusieurs raisons :
La figure ![]() illustre l'effet d'une erreur d'estimation de phase. Les cercles montrent un agrandissement des zones intéressantes. L'erreur d'estimation peut être caractérisée de deux manières équivalentes :
illustre l'effet d'une erreur d'estimation de phase. Les cercles montrent un agrandissement des zones intéressantes. L'erreur d'estimation peut être caractérisée de deux manières équivalentes :
Afin d'observer cette erreur d'amplitude, il est nécessaire de comparer le signal angulaire estimé à un signal de référence. Ce signal de référence sera d'abord obtenu en re-échantillonnant ce même signal accéléromètrique mais en utilisant une démodulation du signal issu du codeur optique. Ensuite, ces signaux seront comparés au signal acquis simultanément dans le domaine angulaire à l'aide d'une autre chaîne d'acquisition.
La figure ![]() montre le spectre du signal issu du codeur optique. Ce spectre contient des bandes latérales espacées de
montre le spectre du signal issu du codeur optique. Ce spectre contient des bandes latérales espacées de ![]() par rapport à la fréquence centrale (
par rapport à la fréquence centrale (![]() est la période de rotation de l'arbre d'entrée). Elles correspondent à une modulation de fréquence du signal codeur optique par la vitesse de l'arbre d'entrée (phénomène de balourd). Cette fluctuation de vitesse ne respecte pas les contraintes imposées par l'équation (
est la période de rotation de l'arbre d'entrée). Elles correspondent à une modulation de fréquence du signal codeur optique par la vitesse de l'arbre d'entrée (phénomène de balourd). Cette fluctuation de vitesse ne respecte pas les contraintes imposées par l'équation (![]() ) qui définit la fluctuation de vitesse maximale. La figure
) qui définit la fluctuation de vitesse maximale. La figure ![]() compare les estimations de vitesse basées sur le pic central (dénommées BF et correspondant à la précision du top tour) et celles incluant les bandes latérales (HF). La modulation de fréquence apparaît clairement sur
compare les estimations de vitesse basées sur le pic central (dénommées BF et correspondant à la précision du top tour) et celles incluant les bandes latérales (HF). La modulation de fréquence apparaît clairement sur ![]() .
. ![]() correspond à une fréquence moyennée. Comme le signal accéléromètrique est filtré en utilisant un filtre similaire à
correspond à une fréquence moyennée. Comme le signal accéléromètrique est filtré en utilisant un filtre similaire à ![]() (pour éviter les fréquences parasites), les fréquences instantanées résultantes sont très proches (voir figure
(pour éviter les fréquences parasites), les fréquences instantanées résultantes sont très proches (voir figure ![]() ).
).
La figure ![]() montre la superposition des signaux re-échantillonnés en utilisant respectivement le codeur (version BF et HF) ainsi que la
montre la superposition des signaux re-échantillonnés en utilisant respectivement le codeur (version BF et HF) ainsi que la
![]() harmonique du signal accéléromètrique (notée
harmonique du signal accéléromètrique (notée ![]() ). Malgré la modulation de fréquence présente uniquement dans
). Malgré la modulation de fréquence présente uniquement dans ![]() , les signaux sont assez proches. Dès lors, il serait intéressant d'étudier l'impact de cette différence de fréquence instantanée sur l'instant d'échantillonnage ou encore l'erreur dans l'instant d'échantillonnage
, les signaux sont assez proches. Dès lors, il serait intéressant d'étudier l'impact de cette différence de fréquence instantanée sur l'instant d'échantillonnage ou encore l'erreur dans l'instant d'échantillonnage
![]() présentée sur la figure
présentée sur la figure ![]() .
.
Pour évaluer ![]() , une droite d'équation
, une droite d'équation
![]() est re-échantillonnée dans le domaine angulaire en utilisant respectivement l'information de phase extraite du signal accéléromètrique (
est re-échantillonnée dans le domaine angulaire en utilisant respectivement l'information de phase extraite du signal accéléromètrique (![]() ) et du codeur (
) et du codeur (![]() et
et ![]() ). On obtient un instant d'échantillonnage en fonction de l'angle. L'erreur d'instant d'échantillonnage est alors obtenue en calculant les différences entre les instants d'échantillonnage issus de deux signaux distincts.
). On obtient un instant d'échantillonnage en fonction de l'angle. L'erreur d'instant d'échantillonnage est alors obtenue en calculant les différences entre les instants d'échantillonnage issus de deux signaux distincts.
La figure ![]() montre l'écart entre le re-échantillonnage basé sur signal accéléromètrique (
montre l'écart entre le re-échantillonnage basé sur signal accéléromètrique (![]() ) et celui basé sur le signal codeur. L'effet de la modulation de fréquence présente dans le signal codeur peut être vu sur la courbe en trait fin comparant
) et celui basé sur le signal codeur. L'effet de la modulation de fréquence présente dans le signal codeur peut être vu sur la courbe en trait fin comparant ![]() et
et ![]() . La courbe correspondant au codeur
. La courbe correspondant au codeur ![]() ne contient plus les ``hautes'' fréquences associées à la modulation mais correspond à une fréquence moyenne puisque le filtrage préalable au calcul du signal analytique a exclu les bandes latérales (voir figures
ne contient plus les ``hautes'' fréquences associées à la modulation mais correspond à une fréquence moyenne puisque le filtrage préalable au calcul du signal analytique a exclu les bandes latérales (voir figures ![]() ). On peut constater que la principale cause d'erreur est due à ce filtrage. Il existe une erreur systèmatique de
). On peut constater que la principale cause d'erreur est due à ce filtrage. Il existe une erreur systèmatique de ![]() équivalent à un déphasage d'environ
équivalent à un déphasage d'environ ![]() degrés. Nous ne nous intéressons pas à cette erreur puisqu'en pratique la référence ``zéro degré'' est obtenue, si elle est souhaitée, en re-échantillonnant le signal top tour, qui est donc sujet au même déphasage.
degrés. Nous ne nous intéressons pas à cette erreur puisqu'en pratique la référence ``zéro degré'' est obtenue, si elle est souhaitée, en re-échantillonnant le signal top tour, qui est donc sujet au même déphasage.
L'erreur maximale entre deux instants d'échantillonnage est de ![]() (crête à crête) (figure
(crête à crête) (figure ![]() ). Si la vitesse était constante, les
). Si la vitesse était constante, les ![]() fronts montants fournis par le codeur (c'est-à-dire
fronts montants fournis par le codeur (c'est-à-dire ![]() échantillons par tour) correspondraient à une période d'échantillonnage de
échantillons par tour) correspondraient à une période d'échantillonnage de ![]() . Dès lors, si l'on considère que le re-échantillonnage angulaire basé sur le codeur est parfait, l'erreur d'échantillonnage de
. Dès lors, si l'on considère que le re-échantillonnage angulaire basé sur le codeur est parfait, l'erreur d'échantillonnage de ![]() correspond à
correspond à ![]() échantillons dans le domaine angulaire. Ainsi, l'écart sur la fréquence instantanée et la vitesse de rotation bien que spectaculaire n'a que peu d'influence sur la précision.
échantillons dans le domaine angulaire. Ainsi, l'écart sur la fréquence instantanée et la vitesse de rotation bien que spectaculaire n'a que peu d'influence sur la précision.
Une acquisition angulaire (![]() échantillons par tour) a été effectuée en parallèle avec l'acquisition temporelle afin d'évaluer rigoureusement la qualité du re-échantillonnage a posteriori. La figure
échantillons par tour) a été effectuée en parallèle avec l'acquisition temporelle afin d'évaluer rigoureusement la qualité du re-échantillonnage a posteriori. La figure ![]() montre les différences entre les deux signaux. Les agrandissements dans les cercles permettent de noter les différences entre les deux signaux. Il est important de noter qu'il n'est pas possible de caractériser l'erreur d'échantillonnage dans ce cas puisque l'échantillonnage angulaire supprime l'information de phase ou vitesse (incrément angulaire ou écart de phase constant entre chaque point). La seule évaluation possible utilisant le signal codeur optique enregistré en fonction du temps a déjà été faite sur la figure
montre les différences entre les deux signaux. Les agrandissements dans les cercles permettent de noter les différences entre les deux signaux. Il est important de noter qu'il n'est pas possible de caractériser l'erreur d'échantillonnage dans ce cas puisque l'échantillonnage angulaire supprime l'information de phase ou vitesse (incrément angulaire ou écart de phase constant entre chaque point). La seule évaluation possible utilisant le signal codeur optique enregistré en fonction du temps a déjà été faite sur la figure ![]() .
.
Au paragraphe ![]() nous avons montré l'effet du bruit sur l'estimation de la phase. Afin d'observer cette influence, un bruit blanc gaussien a été ajouté au signal accéléromètrique. Le rapport signal sur bruit a été corrigé afin de tenir compte du filtrage passe-bande autour de
nous avons montré l'effet du bruit sur l'estimation de la phase. Afin d'observer cette influence, un bruit blanc gaussien a été ajouté au signal accéléromètrique. Le rapport signal sur bruit a été corrigé afin de tenir compte du filtrage passe-bande autour de ![]() . Ce rapport signal sur bruit ne prend malheureusement pas en compte le bruit initial qui est supposé faible. La phase est ensuite estimée en utilisant la méthode basée sur le signal analytique. L'erreur de phase s'obtient en retranchant la phase estimée à la phase associée au signal sans bruit additif. La moitié de l'amplitude de la fluctuation totale (maximum-minimum) est ensuite utilisée pour obtenir un équivalent à
. Ce rapport signal sur bruit ne prend malheureusement pas en compte le bruit initial qui est supposé faible. La phase est ensuite estimée en utilisant la méthode basée sur le signal analytique. L'erreur de phase s'obtient en retranchant la phase estimée à la phase associée au signal sans bruit additif. La moitié de l'amplitude de la fluctuation totale (maximum-minimum) est ensuite utilisée pour obtenir un équivalent à ![]() (voir figure
(voir figure ![]() ). On obtient alors une mesure pour un rapport signal sur bruit donné. Afin d'évaluer la pertinence et la dispersion de cette mesure, le processus est répété
). On obtient alors une mesure pour un rapport signal sur bruit donné. Afin d'évaluer la pertinence et la dispersion de cette mesure, le processus est répété ![]() fois pour un même rapport signal sur bruit.
fois pour un même rapport signal sur bruit.
La figure ![]() montre l'évolution de l'écart type de l'erreur de la phase en fonction du rapport signal sur bruit. La courbe a été obtenue à l'aide d'une régression de la forme
montre l'évolution de l'écart type de l'erreur de la phase en fonction du rapport signal sur bruit. La courbe a été obtenue à l'aide d'une régression de la forme
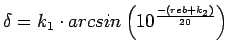 . Seule la zone
. Seule la zone
![]() est affichée car les valeurs inférieures à
est affichée car les valeurs inférieures à ![]() présentent une trop grande dispersion. Plus le rapport signal sur bruit est faible, plus les écarts types sont dispersés. En effet, sur la figure
présentent une trop grande dispersion. Plus le rapport signal sur bruit est faible, plus les écarts types sont dispersés. En effet, sur la figure ![]() , le cercle contenant toutes les valeurs possibles du bruit se rapproche de l'origine, sa contribution ainsi que sa variance se trouvent amplifiées. Du point de vue mathématique, la pente de la courbe étant plus importante lorsque l'on se rapproche de
, le cercle contenant toutes les valeurs possibles du bruit se rapproche de l'origine, sa contribution ainsi que sa variance se trouvent amplifiées. Du point de vue mathématique, la pente de la courbe étant plus importante lorsque l'on se rapproche de ![]() , une fluctuation ``locale'' du rapport signal sur bruit produira une fluctuation plus importante de l'écart type. Comme l'indique la valeur de
, une fluctuation ``locale'' du rapport signal sur bruit produira une fluctuation plus importante de l'écart type. Comme l'indique la valeur de ![]() , il existe un écart de
, il existe un écart de ![]() entre cette courbe et la courbe théorique (figure
entre cette courbe et la courbe théorique (figure ![]() ), cet écart est probablement causé par le bruit présent initialement. Il expliquerait également la forte dispersion avant
), cet écart est probablement causé par le bruit présent initialement. Il expliquerait également la forte dispersion avant ![]() . Le facteur
. Le facteur ![]() montre que l'on suit la loi à une translation près.
montre que l'on suit la loi à une translation près.
Néanmoins, le niveau du bruit restant inconnu en pratique, il est impossible de prévoir son influence. Le bruit n'est pas blanc mais filtré (chemin de transmission, résonnances, ...), ces calculs justifient la nécessité d'utiliser le plus grand nombre d'harmoniques possibles pour estimer la phase instantannée.
La méthode cepstrale est bien plus simple à utiliser puisqu'il est seulement nécessaire de lui fournir une période de rotation moyenne ainsi qu'une bande d'intérêt qui peut être trouvée de manière empirique.
La figure ![]() montre l'erreur d'amplitude. Elle a été partagée en trois zones séparées par un pointillé correspondant respectivement au début, au milieu et à la fin du signal. Les deux signaux sont assez proches. Ainsi, le cepstre remplace avantageusement un top tour pour cet exemple.
montre l'erreur d'amplitude. Elle a été partagée en trois zones séparées par un pointillé correspondant respectivement au début, au milieu et à la fin du signal. Les deux signaux sont assez proches. Ainsi, le cepstre remplace avantageusement un top tour pour cet exemple.
La figure ![]() montre l'erreur d'instant d'échantillonnage. Contrairement à la méthode de re-échantillonnage basée sur la démodulation autour d'une fréquence d'engrènement, l'écart d'échantillonnage entre le cepstre et le codeur
montre l'erreur d'instant d'échantillonnage. Contrairement à la méthode de re-échantillonnage basée sur la démodulation autour d'une fréquence d'engrènement, l'écart d'échantillonnage entre le cepstre et le codeur ![]() ne comporte pas majoritairement de composante basse fréquence. A chaque estimation la position du pic cepstrale est estimée à un échantillon près (après interpolation). Dès lors, cette imprécision génère une erreur d'estimation blanche et non basse fréquence comme pour la méthode précédente. Ici l'erreur d'échantillonnage a une amplitude crête à crête maximale de
ne comporte pas majoritairement de composante basse fréquence. A chaque estimation la position du pic cepstrale est estimée à un échantillon près (après interpolation). Dès lors, cette imprécision génère une erreur d'estimation blanche et non basse fréquence comme pour la méthode précédente. Ici l'erreur d'échantillonnage a une amplitude crête à crête maximale de ![]() soit une précision moindre que pour la méthode précédente. Cette erreur pourrait sans doute être diminuée en améliorant la méthode d'estimation de la position du pic du cepstre.
soit une précision moindre que pour la méthode précédente. Cette erreur pourrait sans doute être diminuée en améliorant la méthode d'estimation de la position du pic du cepstre.
Cette méthode est basée sur la ressemblance des signaux. Dès lors, elle est sensible aux fluctuations de vitesse. En effet, si la fluctuation de vitesse se révèle trop importante, les signaux ne se ressembleront plus d'un tour à l'autre et leur ``écho'' sera moins facilement détectable par le cepstre.
Afin d'étudier l'influence du bruit, nous ajoutons au signal vibratoire normalisé un bruit additif dans un rapport donné. La phase est ensuite estimée par la méthode cepstrale. L'erreur de phase est estimée en calculant l'écart avec la phase de référence obtenue par démodulation du signal codeur ![]() . L'amplitude crête-à-crête de cet écart est ensuite mémorisée. Plusieurs mesures sont réalisées pour un même rapport signal sur bruit.
. L'amplitude crête-à-crête de cet écart est ensuite mémorisée. Plusieurs mesures sont réalisées pour un même rapport signal sur bruit.
La figure ![]() montre l'évolution de l'erreur d'amplitude en fonction du rapport signal sur bruit. Cette courbe permet de vérifier la moindre sensibilité au bruit du cepstre robuste. Le cepstre robuste est néanmoins plus long à calculer (un calcul de corrélation en plus). Contrairement à la méthode basée sur le signal analytique où la précision se dégrade progressivement, un bruit trop important rend le pic indétectable et provoque une erreur non négligeable. Une fois que le rapport signal sur bruit est acceptable, l'erreur de phase varie peu : quand l'amplitude du pic est suffisamment importante pour être détectée, la diminution du bruit n'apporte plus d'amélioration.
montre l'évolution de l'erreur d'amplitude en fonction du rapport signal sur bruit. Cette courbe permet de vérifier la moindre sensibilité au bruit du cepstre robuste. Le cepstre robuste est néanmoins plus long à calculer (un calcul de corrélation en plus). Contrairement à la méthode basée sur le signal analytique où la précision se dégrade progressivement, un bruit trop important rend le pic indétectable et provoque une erreur non négligeable. Une fois que le rapport signal sur bruit est acceptable, l'erreur de phase varie peu : quand l'amplitude du pic est suffisamment importante pour être détectée, la diminution du bruit n'apporte plus d'amélioration.
Dans ce chapitre, nous avons re-échantillonnés les signaux en vu d'induire la cyclostationnarité. Il existe également d'autres approches visant à extraire le contenu cyclique du signal.
Par exemple, le filtre de Vold-Kalman [#!herlufsen:characteristics!#,#!vold:multi!#] effectue un suivi d'ordre dans le domaine temporel. Pour cela, le signal est modélisé comme une série d'amplitudes
![]() modulant des exponentielles
modulant des exponentielles
![]() . Les fréquences associés à ces exponentelles représentent les fréquences de rotation du système ainsi que leurs différentes harmoniques.
A l'aide d'une estimation de la phase
. Les fréquences associés à ces exponentelles représentent les fréquences de rotation du système ainsi que leurs différentes harmoniques.
A l'aide d'une estimation de la phase ![]() réalisé a partir d'un signal tachymétrique, le filtre de Vold-Kalman estime la série d'amplitude composantes
réalisé a partir d'un signal tachymétrique, le filtre de Vold-Kalman estime la série d'amplitude composantes
![]() .
Cette méthode ne fournit pas de signaux dans le domaine angulaire mais uniquement les composantes modulantes.
.
Cette méthode ne fournit pas de signaux dans le domaine angulaire mais uniquement les composantes modulantes.
Dans [#!granjon:modelisation!#], Granjon propose une méthode d'extraction des composantes ``périodiques'' associées à la rotation de la machine. Cette méthode nécessite un signal de référence à la fréquence de rotation de la machine (top tour, ...). En minimisant l'erreur quadratique entre le signal de référence filtré par un filtre périodique (cf. chapitre 5) et le signal vibratoire, il estime la composante périodique synchrone de la machine tournante. Cette méthode reste limité à l'ordre ![]() (partie périodique).
(partie périodique).
Nous avons présenté, en plus des méthodes classiques, deux nouvelles méthodes pour réaliser un re-échantillonnage a posteriori basé sur les signaux accélérométriques. La première basée sur la démodulation autour de la fréquence d'engrènement et la seconde basée sur les similitudes (cepstre). Ces deux méthodes fournissent une précision équivalente à celle du top tour. Malgré cela, l'erreur entre les signaux acquis angulairement et les signaux re-échantillonnés est restée relativement faible lors de nos expérimentations. L'intérêt majeur de ces méthodes est le fait de pouvoir se passer de codeur. Les deux méthodes nécessitent quelques connaissances a priori sur la cinématique de la machine et la vitesse de rotation. Néanmoins, nous ne considérons pas ce point comme un handicap puisqu'elles sont nécessaires lors du diagnostic si l'on veut exploiter la cyclostationnarité. Nos méthodes ne fonctionnent que pour une vitesse moyenne stable (seule les fluctuations de vitesse de quelques pour mille inhérentes à la machine sont tolérées). L'atout majeur du re-échantillonnage a posteriori est de pouvoir combiner les avantages de l'observation double dans le domaine angulaire (nombre de points par tour constant, signal cyclostationnaire) et dans le domaine temporel (étude de la fluctuation de vitesse pour le diagnostic).
La méthode basée sur le cepstre est plus générale puisqu'elle exploite les similitudes, elle pourra donc être envisagée pour de nombreux types de signaux cyclostationnaires à l'ordre ![]() . Néanmoins, elle est beaucoup plus sensible au rapport signal à bruit que la méthode basée sur la démodulation d'harmoniques. Un meilleur algorithme de détection du pic dans le cepstre permettrait peut-être d'améliorer cette précision. Bien qu'à première vue la courbe
. Néanmoins, elle est beaucoup plus sensible au rapport signal à bruit que la méthode basée sur la démodulation d'harmoniques. Un meilleur algorithme de détection du pic dans le cepstre permettrait peut-être d'améliorer cette précision. Bien qu'à première vue la courbe ![]() soit plus intéressante que la courbe
soit plus intéressante que la courbe ![]() , il n'en est rien : l'erreur présentée dans la courbe
, il n'en est rien : l'erreur présentée dans la courbe ![]() correspond à l'erreur sur l'harmonique de l'engrènement étudiée. Pour la ramener à une erreur sur la position de l'arbre de sortie, il convient de la diviser par le rang de l'harmonique ainsi que par le nombre de dents de la roue qui engrène. On obtient alors une erreur très faible.
correspond à l'erreur sur l'harmonique de l'engrènement étudiée. Pour la ramener à une erreur sur la position de l'arbre de sortie, il convient de la diviser par le rang de l'harmonique ainsi que par le nombre de dents de la roue qui engrène. On obtient alors une erreur très faible.
Il serait intéressant d'étendre ces méthodes à la vitesse variable. Pour ce faire, on pourrait découper le signal en portions où la variation de vitesse serait considérée comme faible. Il est aussi envisageable d'effectuer un suivi peu précis afin de compenser grossièrement les fluctuations de vitesse, puis, de travailler avec les méthodes présentées ici sur le signal avec les fluctuations de vitesse compensées (re-échantillonnage a posteriori itératif).
Il faut noter qu'à l'heure actuelle, la tendance chez les fabricants de machines tournantes est d'intégrer des codeurs angulaires dans leurs produits dans le but de pouvoir réaliser différents types de contrôles (asservissement de vitessse, position, ...). Une mise a disposition de ces signaux permettrait d'une part de réaliser des acquisitions sous échantillonnage angulaires directement sans contraintes supplémentaires ; et d'autre part d'intégrer le concept de diagnostic dans les variateurs de vitesse, ...