1. Cyclostationnarités : Définitions et propriétés

1.1 Pourquoi la cyclostationnarité (Avant propos)

Les outils de traitement du signal sont souvent utilisés dans le contexte stationnaire. Néanmoins, dans des domaines tels que la communication, le traitement de la parole, la mécanique, ... les hypothèses simplificatrices permettant de travailler dans un contexte stationnaire ne sont plus valables.

Figure: Exemple de signal cyclostationnaire

Pour illustrer cela, la figure montre un signal vibratoire issu d'un réducteur à engrenages. Nous pouvons noter la présence d'un motif d'allure périodique dans le signal. La période est indiquée par des rectangles alternativement noirs et blancs. Cette périodicité apparente est due à l'existence d'un cycle de base que l'on rencontre dans la plupart des systèmes mécaniques et en particulier dans les machines tournantes. Si les paramètres de fonctionnement de la machine sont constants (vitesse moyenne, pression, température, durée du cycle moteur, période du réducteur) on dira que les signaux qui en sont issus sont cyclostationnaires. Mathématiquement, un signal est cyclostationnaire si l'on trouve des périodicités dans certaines de ses statistiques. Chaque période ou cycle peut être considéré comme la réalisation d'un même processus aléatoire. Pour cela, chaque réalisation doit débuter à une position angulaire identique (même position de l'arbre pour un moteur électrique, même dents en contact pour les engrenages, ...). Si l'on superpose ces réalisations, on pourra alors calculer la moyenne d'ensemble (c'est-à-dire l'amplitude moyenne pour un angle $\theta$ donné) comme le montre la figure . Cette moyenne d'ensemble, permettra d'extraire la ``partie périodique'' du signal (à l'ordre $1$). Lorsque cette dernière existe, le signal sera alors cyclostationnaire à l'ordre 1.

Ce signal a été choisi car il permet de visualiser facilement ces périodicités. La partie périodique peut être noyée dans du bruit. Il faut alors utiliser la moyenne d'ensemble pour faire ressortir ce motif périodique par rapport au bruit (si ce bruit est stationnaire). En pratique, on ne disposera souvent que d'une seule réalisation et on sera conduit à remplacer la moyenne d'ensemble par une moyenne de cycles appelée moyenne synchrone (sous réserve d'existence).

Figure: Moyenne d'ensemble

Certains signaux de communication bien que non périodiques (à l'ordre 1), ont une énergie périodique. La figure inspirée de [#!max:methodes!#] présente un tel signal. Une fois élevé au carré, il devient périodique. On dira alors que ce signal présente des périodicités cachées. Un tel signal est cyclostationnaire à l'ordre 2. De façon plus générale, un signal est cyclostationnaire à l'ordre 2 si ses propriétés statistiques à l'ordre 2 sont périodiques.

Figure: Signal cyclostationnaire à l'ordre 2

La cyclostationnarité, cas particulier de la non-stationnarité nous permettra donc de mieux appréhender les périodicités cachées ou non d'un signal. Les machines tournantes générant intrinsèquement des périodicités, on aura intérêt à exploiter la cyclostationnarité.

Après avoir expliqué brièvement l'intérêt de la cyclostationnarité nous allons maintenant en présenter l'aspect théorique.

1.2 Cyclostationnarité

Les premières études sur la cyclostationnarité datent des années 1950 avec les travaux précurseurs de Benett [#!bennett:statistics!#] et Gladyshev [#!gladyshev:periodically1!#,#!gladyshev:periodically2!#]. Comme le montre la figure (issue de [#!gardner:cyclostationarity!#]) et la figure , la cyclostationnarité a commencé à susciter un intérêt croissant à partir des années $1980$ (explosion du domaine des télécommunications, ...). Elle a été utilisée dans l'identification, la séparation de sources, la séparation de signaux se recouvrant spectralement, ... Néanmoins, la cyclostationnarité n'a pas suscité le même engouement en mécanique : son utilisation dans ce domaine et en particulier pour les machines tournantes n'est apparue que récemment. Ce manque d'enthousiasme est probablement dû aux variations de vitesse des systèmes mécaniques qui ont tendance à supprimer la cyclostationnarité. D'autre part, il existe souvent une forte cyclostationnarité à l'ordre $1$ qu'il est ardu de retrancher car sa période n'est pas forcément stable et connue. Il est alors difficile d'exploiter directement les outils développés dans le domaine des télécommunications où les signaux sont souvent à moyenne synchrone nulle. La cyclostationnarité a ouvert des perspectives et a permis d'obtenir des résultats très intéressants [#!lejeune:cyclostationnarites!#,#!mccormick:cyclostationarity!#,#!dalpiaz:effectiveness!#,#!capdessus:aide!#,#!capdessus:cyclostationary!#,#!randall:relationship!#,#!bouillaut:cyclostationary!#,#!antoni:effective1!#,#!antoni:cyclostationary!#,#!raad:contributions!#].

Figure: Nombre d'articles sur la cyclostationnarité (1955-2004)

Tout comme pour la stationnarité, nous allons définir la cyclostationnarité à l'ordre $n\ge1$. Pour cela nous devons tout d'abord rappeler la définition des moments et cumulants dans le contexte cyclostationnaire.

1.2.1 Moments et Cumulants

Puisque nous nous interéssons plus particulièrement aux machines tournantes, nous allons utiliser leur variable générique : l'angle $\theta$ au lieu du temps $t$. Pour plus de simplicité, nous nous limiterons aux vecteurs aléatoires réels. Le cas des vecteurs aléatoires complexes est traité notamment dans [#!lacoume:statistiques!#,#!amblard:statistics!#].

Soit un vecteur aléatoire $\vect{X}\left(\vect{\theta}\right)=\left[X_1\left(\theta_1\right),\cdots,X_N\left(\theta_N\right)\right]$ de dimension $N$ à valeurs réelles admettant comme fonction de répartition $\frep{\vect{X}}\left(\vect{v},\vect{\theta}\right)$ (avec $\vect{v}=\left[v_1,\cdots,v_N\right]\in \mathbb{R}^N$ et $\vect{\theta}\in \mathbb{R}^N$) définie par :

$$\frep{\vect{X}}\left(\vect{v},\vect{\theta}\right) = P \lef... ...ight)\leq v_1,\cdots,X_N\left(\theta_N\right)\leq v_N\right\}$$ (1.1)

Il est important de noter que nous travaillons pour l'instant sur des réalisations de $X$ et que nous n'avons fait aucune hypothèse quant à l'ergodicité. A partir de ce vecteur aléatoire, il est alors possible de définir la fonction caractéristique qui n'est autre que la transformée de Fourier de la densité de probabilité (à $2\pi$ près).

$$\fcar{\vect{X}}\left(\vect{u},\vect{\theta}\right) \triangleq \esp{e^{j\vect{X\left(\vect{\theta}\right)}^T \vect{u}}}$$ (1.2)

$$= \int_{\mathbb{R}^N}e^{j\vect{v}^T \vect{u}} \; d\frep{\vect{X}}\left(\vect{v},\vect{\theta}\right)$$ (1.3)

Où $d \frep{\vect{X}}\left(\vect{v},\vect{\theta}\right)$ désigne la différentielle de la fonction de répartition. Ici nous utilisons la fonction de répartition plutôt que la densité de probabilité. En effet, à une fonction de répartition pourra correspondre une distribution de densité de probabilité (par exemple si la fonction de répartition est un échelon). Cette fonction de répartition peut être décomposée en une somme de deux termes et écrite sous la forme :

$$\frep{\vect{X}}\left(\vect{v},\vect{\theta}\right) = \frep{... ... %+ \frep{\vect{X}}_s\left(\vect{\omega},\vect{\theta}\right)$$ (1.4)

$\frep{\vect{X}}_c\left(\vect{v},\vect{\theta}\right)$ étant la partie continue et dérivable, et, $\frep{\vect{X}}_d\left(\vect{v},\vect{\theta}\right)$ une fonction de type escalier. La première fonction caractéristique correspondra à une variable aléatoire continue, la deuxième à une variable aléatoire discrète. Ainsi, cette formulation permettra de traiter à la fois le cas discret et le cas continu.

On définit également la seconde fonction caractéristique par:

$$\sfcar{\vect{X}}\left(\vect{u},\vect{\theta}\right)=\ln \fcar{\vect{X}}\left(\vect{u},\vect{\theta}\right)$$ (1.5)

Il est alors possible de développer les fonctions caractéristiques en série entière. Les coefficients de ces séries permettront alors de retrouver les moments pour $\fcar{\vect{X}}\left(\vect{u},\vect{\theta}\right)$ et les cumulants pour $\sfcar{\vect{X}}\left(\vect{u},\vect{\theta}\right)$.

1.2.1.1 Moments

Pour tout n-uplet $\left(i_1,\cdots,i_N\right)\in \mathbb{R}^N$ tel que $\sum_{n=1}^N i_n=k$, le moment d'ordre $k$ est défini par:

$$\esp{\prod_{n=1}^N X_n^{i_n}\left(\theta_n\right)}=\int_{\m... ..._n^{i_n} d \frep{\vect{X}}\left(\vect{v},\vect{\theta}\right)$$ (1.6)

On pourra retrouver également les moments à partir de la fonction caractéristique:

$$\fcar{\vect{X}}\left(\vect{u},\vect{\theta}\right) = \sum_{k=0}^{\infty} \frac{j^k}{k!} \esp{\left(\vect{u}^T\vect{X}\left(\vect{\theta}\right)\right)^k}$$ (1.7)

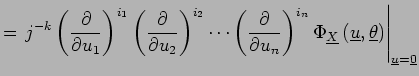$$\Rightarrow \esp{\prod_{n=1}^N X_n^{i_n}\left(\theta_n\right)} = \left. j^{-k} \left(\derp{}{u_1}\right)^{i_1} \left(\derp{}{u_2... ...ar{\vect{X}}\left(\vect{u},\vect{\theta}\right)\right\vert _{\vect{u}=\vect{0}}$$ (1.8)

Comme on se place dans le cas de vecteurs aléatoires, choisir un $i_n> 1$ équivaut à utiliser un vecteur aléatoire contenant plusieurs fois la même variable aléatoire. On se limitera donc à $k=N$ et $i_n=1$ $\forall n\in\left[1;N\right]$. On pourra alors définir la notation :

$$\momns{\vect{X}}{k}{\vect{\theta}} \triangleq \esp{\prod_{n... ...\vect{u},\vect{\theta}\right)\right\vert _{\vect{u}=\vect{0}}$$ (1.9)

Par exemple, la variance sera interprétée comme la covariance de deux vecteurs identiques et pourra être notée $\momns{\left[X,X\right]}{k}{\vect{\theta}}$.

Dans le cas d'un vecteur aléatoire, l'ordre $\left(k\right)$ pourra être omis pour $k=N$.

1.2.1.2 Cumulants

En utilisant exactement la même procédure mais à partir de la seconde fonction caractéristique, nous obtenons les cumulants. Pour les mêmes raisons, nous choisirons d'utiliser les cumulants simples c'est-à-dire avec $i_n=1$ $\forall n\in\left[1;N\right]$. Nous aurons alors :

$$\cumns{\vect{X}}{k}{\vect{\theta}} \triangleq \left.\left(-... ...\vect{u},\vect{\theta}\right)\right\vert _{\vect{u}=\vect{0}}$$ (1.10)

Il est important de noter que nous utilisons $\cumns{\vect{X}}{k}{\vect{\theta}}$ et non $\cum{\vect{X}}{k}$ puisque nous ne nous plaçons pas dans le contexte stationnaire. Pour un signal unidimensionnel, nous avons $\cumns{X}{k}{\vect{\theta}}=\cumns{\vect{Y}}{k}{\vect{\theta}}$ où $\vect{Y}$ est un vecteur contenant $k$ fois la variable aléatoire $X$ : $\vect{Y}=\underbrace{\left[X,\cdots,X\right]}_{k fois}$.

1.2.1.3 Relation moments cumulants

Il est possible d'exprimer les cumulants d'ordre $N$ en fonction des moments à l'aide de la formule de Leonov et Shiryaev [#!leonov:method!#] en utilisant les $I$ partitions $P_{N_i}=\left\{\nu_{1_i},\cdots,\nu_{q_i}\right\}$ de l'ensemble $\left\{1,\cdots,N\right\}$ :

$$\cumns{\vect{X}}{N}{\vect{\theta}} = \sum_{i=1}^{I} \left(-... ...q_i} \momnsr{\vect{X}_{\nu_{j_i}}}{\vect{\theta}_{\nu_{j_i}}}$$ (1.11)

Par exemple, à l'ordre 2, on a $P_{N_1}=\left\{\left\{1,2\right\}\right\}$ et $P_{N_2}=\left\{\left\{1\right\},\left\{2\right\}\right\}$ d'où :

$$\cumns{\vect{X}}{2}{\vect{\theta}} = \left(-1\right)^0 0!\momnsr{\vect{X}_{1,2}}{\vect{\theta}_{1,2}} ... ...)^1 1!\momnsr{\vect{X}_1}{\vect{\theta}_1} \momnsr{\vect{X}_2}{\vect{\theta}_2}$$

$$= \momnsr{\vect{X}}{\vect{\theta}} - \momnsr{X_1}{\theta_1} \momnsr{X_2}{\theta_2}$$ (1.12)

On a également :

$$\cumns{\vect{X}}{3}{\vect{\theta}} = \momnsr{\vect{X}}{\vect{\theta}}$$

$$- \momnsr{X_1}{\theta_1} \cdot \momnsr{\vect{X}_{2,3}}{\vect{\theta... ...,3}} -\momnsr{X_3}{\theta_3} \cdot \momnsr{\vect{X}_{1,2}}{\vect{\theta}_{1,2}}$$

$$+ 2 \momnsr{X_1}{\theta_1} \cdot \momnsr{X_2}{\theta_2} \cdot \momnsr{X_3}{\theta_3}$$ (1.13)

Ces formules se simplifient en utilisant des signaux centrés^1.1 pour lesquels $\momns{X_i}{1}{\theta_i}~=~0~\;~\forall i$. Jusqu'à l'ordre $3$, le cumulant correspond au moment calculé sur le signal centré. Le contexte cyclostationnaire nous empêche de simplifier plus ces formules puisque $\momns{X_1}{1}{\theta_1}\neq\momns{X_2}{1}{\theta_2}$.

Cette formule montre que les cumulants d'ordre $N$ dépendent uniquement des moments d'ordre inférieur.

Il est également possible d'exprimer les moments à partir des cumulants :

$$\momns{\vect{X}}{N}{\vect{\theta}} = \sum_{i=1}^{I} \prod_{... ...i} \cumnsr{\vect{X}_{\nu_{j_i}}}{\vect{\theta}_{\nu_{j_i}}}$$ (1.14)

On peut en déduire :

$$\momns{\vect{X}}{2}{\vect{\theta}} = \cumnsr{\vect{X}}{\vect{\theta}} + \cumnsr{X_1}{\theta_1} \cdot \cumnsr{X_2}{\theta_2}$$ (1.15)

$$\momns{\vect{X}}{3}{\vect{\theta}} = \cumnsr{\vect{X}}{\vect{\theta}}$$

$$+ \cumnsr{X_1}{\theta_1} \cdot \cumnsr{\vect{X}_{2,3}}{\vect{\theta... ...3}} + \cumnsr{X_3}{\theta_3} \cdot \cumnsr{\vect{X}_{1,2}}{\vect{\theta}_{1,2}}$$

$$+ \cumnsr{X_1}{\theta_1} \cdot \cumnsr{X_2}{\theta_2} \cdot \cumnsr{X_3}{\theta_3}$$ (1.16)

Tout comme les cumulants, les moments d'ordre $N$ ne sont liés qu'aux cumulants d'ordre inférieur. Après avoir défini les moments et cumulants, nous allons les utiliser afin de caractériser les différents types de cyclostationnarité.

L'utilisation des cumulants permet d'estimer des statistiques qui rendent compte des propriètés à l'ordre $N$ seul, alors que les statistiques issues des moments prennent en compte tous les ordres de $1$ à $N$.

Par exemple, à l'ordre $2$, pour une variable aléatoire $X\left(\theta\right)$, de moyenne $\momnsr{X}{\theta}$ qui peut s'écrire :

$$X\left(\theta\right) = \momnsr{X}{\theta} + X_c\left(\theta... ...ta\right)$\ est la version centrée de $X\left(\theta\right)$}$$ (1.17)

Le cumulant d'ordre $2$ est :

$$\cumnsr{\left[X,X\right]}{\vect{\theta}}=\esp{X_c\left(\the... ... \text{ où $\vect{\theta}=\left[\theta_1, \theta_2\right]$}$$ (1.18)

et le moment d'ordre 2 :

$$\momnsr{\left[X,X\right]}{\vect{\theta}}=\esp{X_c\left(\the... ...\theta_2\right)} +\momnsr{X}{\theta_1} \momnsr{X}{\theta_2}$$ (1.19)

L'équation () montre que le cumulant ne dépend pas de la statistique d'ordre $1$ contrairement au moment d'ordre 2 pour lequel la contribution à l'ordre $1$ est ajoutée (équation ). Le cumulant à l'ordre $2$ retranche donc la contribution issue de l'ordre $1$ et permet ainsi de se focaliser sur l'ordre $2$.

1.2.2 Cyclostationnarité au sens strict

Soit $\pstoch{x}{\theta}{R}$ un processus stochastique complexe ou réel.

$\pstoch{X}{\theta}{R}$ est dit cyclostationnaire au sens strict avec la période cyclique $\Theta$ si sa fonction de répartition est périodique avec la période $\Theta$ :

$$\frep{X}\left(v_1,\cdots,v_n;\theta_1,\cdots,\theta_n\right... ...theta_n+\Theta\right) \text{ $\forall$\ $n\in\mathbb{N^*}$}$$ (1.20)

Que l'on peut écrire de manière plus compacte :

$$\frep{X}\left(\vect{v},\vect{\theta}\right)=\frep{X}\left(\vect{v},\vect{\theta}+\vect{\Theta}\right)$$ (1.21)

La définition de la stationnarité au sens strict peut être retrouvée à partir de cette définition, en supprimant la notion de périodicité. Un processus stochastique $\pstoch{x}{\theta}{R}$ complexe ou réel est dit stationnaire au sens strict si sa fonction de répartition est invariante pour tout changement de l'origine du temps :

$$\frep{X}\left(\vect{v},\vect{\theta}\right)=\frep{X}\left(\... ...ect{\tau}\right) \text{, } \forall \vect{\tau}\in\mathbb{R^N}$$ (1.22)

Dès lors, comme tout signal stationnaire vérifie forcément (), la classe des signaux stationnaires est incluse dans la classe des signaux cyclostationnaires et hérite donc de toutes ses propriétés.

1.2.3 Cyclostationnarité à l'ordre n

$\pstoch{X}{\theta}{R}$ est dit cyclostationnaire à l'ordre n ($\CS{n}$) avec une période cyclique $\Theta$ si son moment d'ordre $n$ existe, et est périodique de période $\vect{\Theta}=\left[\Theta,\cdots,\Theta\right]$:

$$\momns{X}{n}{\vect{\theta}} = \momns{X}{n}{\vect{\theta}+\vect{\Theta}}$$ (1.23)

1.2.4 Cyclostationnarité au sens large

$\pstoch{X}{\theta}{R}$ est dit cyclostationnaire au sens large, s'il est cyclostationnaire conjointement à l'ordre $1$ et à l'ordre $2$.

La définition de la stationnarité au sens large peut être retrouvée à partir de cette définition en supprimant la notion de périodicité : $\pstoch{X}{\theta}{R}$ est dit stationnaire au sens large s'il est stationnaire à l'ordre $1$ et stationnaire à l'ordre $2$.

1.2.5 Cyclostationnarité pure et impure

1.2.5.1 Définition

Soit un signal déterministe $x\left(\theta\right)$ sinusoïdal : $x\left(\theta\right)=sin\left(\theta\right)$. Ce signal est cyclostationnaire à l'ordre $1$ car il est périodique. Son moment d'ordre $n$ est :

$$\momns{x\left(\theta\right)}{n}{\theta_1,\cdots,\theta_n} = \sin\left(\theta_1\right) \sin\left(\theta_2\right) \cdots \sin\left(\theta_n\right)$$ (1.24)

$$= x\left(\theta_n\right) \momns{x\left(\theta\right)}{n-1}{\theta_1,\cdots,\theta_{n-1}}$$ (1.25)

Dans cet exemple très simple, le moment d'ordre $n$ est lié au moment d'ordre inférieur par $x\left(\theta_n\right)$. On a donc affaire à un signal cyclostationnaire à tous les ordres. On ne pourra donc pas étudier séparément l'apport de chaque ordre. On parlera alors de cyclostationnarité ``impure'' puisque $CS_n$ est une conséquence de $CS_{n-1}$.

A l'ordre $2$, il est possible en travaillant sur le signal centré (c'est-à-dire le cumulant) de supprimer l'influence de l'ordre $1$. Par exemple, pour un signal $y\left(\theta\right)=p\left(\theta\right)+r\left(\theta\right)$ composé d'un signal $p\left(\theta\right)$ cyclostationnaire à l'ordre $1$ et d'un autre signal quelconque et indépendant de $p\left(\theta\right)$, le cumulant d'ordre $2$ ne dépendra pas de $p\left(\theta\right)$ contrairement au moment.

$$\cumns{y\left(\theta\right)}{2}{\vect{\theta}} = \momns{\left[y\left(\theta\right)-p\left(\theta\right)\right]}{2}{\vect{\theta}}=\momns{r\left(\theta\right)}{2}{\vect{\theta}}$$ (1.26)

$$\momns{y\left(\theta\right)}{2}{\vect{\theta}} = {\left[\cumns{y\left(\theta\right)}{1}{\vect{\theta}}\right]}^2+\cumns{y\left(\theta\right)}{2}{\vect{\theta}}$$ (1.27)

L'utilisation des cumulants au lieu des moments pourra alors être généralisée aux ordres supérieurs [#!gardner:cumulant!#]. On parlera alors de cyclostationnarité ``pure'' à l'ordre $n$ (noté $\CSP{n}$) puisqu'elle n'entrainera pas $\CSP{n+1}$. On pourra alors caractériser la cyclostationnarité pour un ordre donné indépendamment des autres ordres.

A l'aide de l'équation , il est possible d'établir les implications entre $\CSP{n}$ et $\CS{n}$.

Cyclostationnarité impure à l'ordre ...	... si
2	$\CSP{2}$ ou $\CSP{1}$
3	$\CSP{3}$ ou $\CSP{1}$
4	$\CSP{4}$ ou $\CSP{2}$ ou $\CSP{1}$

1.2.5.2 Illustration

Afin de montrer l'apport des cumulants, nous allons examiner un signal $y\left(\theta\right)$ issu d'un moteur diesel 4 cylindres PSA XUD9 $1905\;cm^3$. Il a été acquis sous échantillonnage angulaire et exploité dans [#!antoni:apports!#,#!antoni:effective1!#,#!antoni:cyclostationary!#]. Ce signal est cyclostationnaire puisque chaque événement mécanique est lié à la position du vilebrequin. Ce signal peut être décomposé en [#!braun:analysis!#]:

$$y\left(\theta\right)=p\left(\theta\right)+cs_2\left(\theta\right)+n\left(\theta\right)$$ (1.28)

• $p\left(\theta\right)$ est une composante $\CS{1}$ de période $4\pi$ (sur un moteur 4 temps le cycle correspond à deux tours de vilebrequin),
• $cs_2\left(\theta\right)$ est la composante cyclostationnaire à l'ordre 2,
• un bruit résiduel $n\left(\theta\right)$.

Les figures à montrent l'apport des cumulants pour caractériser le signal à l'ordre $2$. Le signal analysé ainsi que sa densité spectrale de puissance ont été ajoutés sur les bordures des figures. Parmi les $4$ caractérisations possibles du signal, nous avons choisi la distribution de Wigner-Ville car c'est la transformée de Fourier d'un moment d'ordre $2$. Ce domaine permet de localiser facilement les événements mécaniques. Les figures , , montrent respectivement la distribution de Wigner-Ville associée au moment d'ordre 2 (corrélation), à la moyenne synchrone, et au cumulant d'ordre 2 (variance - on parle alors de spectre de Wigner Ville). L'amplitude des signaux a été normalisée avant les traitements car les calibres utilisés dans la chaîne de mesure n'étaient pas disponibles. Ainsi, nous utilisons $\propto m^2/s^4$ pour indiquer que l'échelle est homogène à des $m^2/s^4$.

Les figures et mettent en évidence que la composante périodique ou $\CS{1}$ du signal est beaucoup plus énergétique que la composante $\CSP{2}$. En conséquence, cette composante domine et provoque des interférences dûes à son caractère déterministe qui nuisent à la lisibilité. Dans la figure , il n'y a que la composante $cs_2$ exempte de toutes interférence détruite par moyennage synchrone de la contribution à l'ordre $2$. L'étude de ces signaux dans [#!antoni:apports!#] a montré l'intérêt de la partie $\CSP{2}$ pour le diagnostic et la localisation des défauts. Il est donc très important et intéressant dans ce cas d'étudier séparément la partie $\CS{1}$ et la partie $\CS{2}$.

Figure: dWV basée sur le moment

Figure: dWV de la moyenne synchrone

Figure: sWV basé sur le cumulant

Cet exemple montre que l'utilisation des cumulants permet d'analyser la contribution de chaque ordre sans être gêné par l'ordre précédent. Jusqu'à l'ordre $3$, l'estimation des cumulants est en théorie assez simple puisqu'il suffit de travailler sur des signaux centrés (débarrassés de leur moyenne synchrone). Nous verrons au cours de cette thèse, qu'en pratique, il n'est pas toujours simple d'enlever cette moyenne (synchrone).

1.3 Extension de la cyclostationnarité

La cyclostationnarité est très intéressante pour étudier les machines tournantes puisqu'elle permet de prendre en compte le caractère cyclique d'un processus. Jusque là nous avons supposé une seule période cyclique. Or, il existe des processus ou des machines qui possèdent plusieurs cycles. Nous allons alors étendre la notion de cyclostationnarité afin de l'adapter à de tels cas.

1.3.1 Presque cyclostationnarité

La presque cyclostationnarité (almost cyclostationary en anglais) [#!gardner:stationarizable!#] est basée sur les fonctions presque périodiques (ou p-périodiques). De telles fonctions sont étudiées dans [#!bass:mathematiques!#,#!corduneanu:almost!#].

1.3.1.1 Fonctions presque périodiques

Une fonction $f:\mathbb{R}\rightarrow\mathbb{C}$ est dite p-périodique sur $\mathbb{C}$ si, pour tout réel $\varepsilon>0$, il existe un polynôme trigonométrique $p_\varepsilon\left(t\right)=\sum_{n=-N}^{N} c_n e^{j\omega_n t}$ ( $c_n \in \mathbb{C},\omega_n \in \mathbb{R}$) tel que :

$$\left\vert f\left(t\right)-p_\varepsilon\left(t\right)\right\vert<\varepsilon \quad \forall t\in \mathbb{R}$$ (1.29)

Où $\omega_n$ est un ensemble de fréquences qui ne sont pas forcément harmoniques entre elles.

On notera alors :

$$f\left(t\right) \approx p\left(t\right) \text{ où $p\left(t\right)$\ est un polynôme trigonométrique}$$ (1.30)

Si la série de Fourier Bohr est uniformément convergente, alors, on peut écrire :

$$f\left(t\right)=p\left(t\right)$$ (1.31)

Dans [#!corduneanu:almost!#], il est montré que la définition () implique que :

Pour tout réel $\varepsilon>0$, il existe un nombre $l\left(\varepsilon\right)$ tel que tout intervalle de longueur $l\left(\varepsilon\right)$ contienne un nombre $\tau$ vérifiant :

$$\left\vert f\left(t+\tau\right)-f\left(t\right)\right\vert<\varepsilon \quad \forall t$$ (1.32)

Cette formulation utilisée dans [#!lacoume:statistiques!#] montre mieux l'aspect ``périodique'' avec l'utilisation de $\tau$. Il est possible de construire une fonction presque périodique en ajoutant $K$ fonctions périodiques $f_k\left(\theta\right)$ ayant des périodes $T_k$ non commensurables entre elles^1.2. Chacune des fonctions périodiques $f_k\left(\theta\right)$ admet alors une décomposition en série de Fourier :

$$f_k\left(\theta\right) = \sum_{m=-\infty}^{\infty} a_{k,m} \cdot e^{2 \pi j m t /T_k}$$ (1.33)

Où $a_{k,m}$ est le coefficient associé à la fréquence $m/T_k$ de la $k^\text{\tiny ième}$ fonction $f_k\left(\theta\right)$ de période $T_k$. Dès lors, on pourra combiner les séries de Fourier associées à chaque fonction :

$$f\left(\theta\right) = \sum_{k=1}^{K} f_k\left(\theta\right... ..._k} = \sum_{n=-\infty}^{\infty} c_n \cdot e^{2 \pi j t \nu_n}$$ (1.34)

Où $c_n$ est le coefficient associé à la fréquence $\nu_n$. Chaque fréquence $\nu_n$ correspond alors à une unique fréquence $m/T_k$. On décompose alors la fonction $f\left(\theta\right)$ sous forme d'une série. Néanmoins, comme les périodes $T_k$ sont incommensurables entre elles (dans notre exemple), les fréquences $\nu_n$, rangées par ordre croissant, ne sont pas en progression linéaire. Il ne s'agit donc plus d'une série de Fourier puisque les $\nu_n$ ne sont pas les harmoniques d'un même fondamental mais d'une décomposition en série de Fourier-Bohr. La fonction $f\left(\theta\right)$ est alors une fonction presque périodique. D'autre part, on ne peut plus écrire $f\left(t\right)=f\left(t+T\right)$ puisqu'il n'existe aucune période commune entre les $T_k$, les fonctions presque-périodiques permettent ainsi de décrire les fonctions comportant plusieurs périodes sans période commune.

1.3.1.2 Presque cyclostationnarité au sens strict

Un processus stochastique $\pstoch{X}{\theta}{R}$ réel est dit presque cyclostationnaire au sens strict si sa fonction de répartition est presque périodique.

1.3.1.3 Déclinaisons de la presque cyclostationnarité

Il sera alors possible de décliner la presque cyclostationnarité à différents ordres en remplaçant périodique par presque périodique. Ainsi, la presque cyclostationnarité au sens large est définie dans [#!gardner:stationarizable!#] par :

Un processus aléatoire centré du second ordre à paramètres réels et continus est presque-cyclostationnaire au sens large si et seulement si, pour tout $\varepsilon>0$, il existe un nombre entier naturel $N_\varepsilon$ et un polynôme trigonométrique à l'ordre $N_\varepsilon$ dans $L^\infty\left(\mathbb{R}\right)$ qui approxime uniformément la fonction d'autocorrélation pour X à $\pm\varepsilon$, c'est-à-dire :

$$\sup_{\tau\in\mathbb{R}}\left\vert\autocorr{X}\left(\theta,... ...)\right\vert<\varepsilon, \quad \forall \theta \in \mathbb{R}$$ (1.35)

On a ainsi une autocorrélation $\autocorr{X}\left(t,\tau\right)$ presque périodique.

Alors que dans le contexte cyclostationnaire nous avions une période, nous avons ici un ensemble de presque périodes $1/\omega_n$ qui peuvent être quelconques. On peut alors en mettant des contraintes sur ces presque périodes faire apparaître des sous-ensembles des signaux presque cyclostationnaires.

1.3.2 Polycyclostationnarité

Parmi les fonctions presques périodiques, les fonctions polypériodiques vont nous permettre de construire un sous-ensemble des processus presque cyclostationnaires : les processus polycyclostationnaires. Nous allons tout d'abord définir la polypériodicité :

Une fonction $f:\mathbb{R}\rightarrow\mathbb{C}$ est dite polypériodique avec les fréquences fondamentales associées $\left\{\nu_i\right\}_{i=1,\cdots,q}$ si elle est presque périodique, et si les fréquences associées aux coefficients de Fourier-Bohr $c_n$ sont toutes multiples des $\nu_i$. L'ensemble $\left\{\nu_i\right\}_{i=1,\cdots,q}$ est tel que $q$ est fini et les $\nu_i$ sont incommensurables.

La polypériodicité impose d'une part un nombre fini de fréquences fondamentales incommensurables et n'est plus définie à l'aide d'une convergence uniforme d'autre part. La fonction $f\left(\theta\right)$ utilisée pour illustrer les fonctions presque périodiques sera donc polypériodique si $K$ est fini. Cette distinction permettra d'être plus proche de la réalité où les fréquences fondamentales sont générées par un nombre fini de procédés physiques.

1.3.2.1 Définition de la polycyclostationnarité

Un processus stochastique $\pstoch{X}{\theta}{R}$ réel est dit polycyclostationnaire ($\polyCS{}$) avec les périodes cycliques $\Theta_i$ si sa fonction de répartition est polypériodique selon ces mêmes périodes.

Nous allons inclure également dans la polycyclostationnarité le cas où les $\Theta_i$ sont rationnels entre eux (commensurables). Dès lors, il convient d'envisager 2 cas.

1.3.2.2 Périodes cycliques rationnelles

Si les périodes cycliques $\left\{T_n\right\}_{n=1\cdots N}$ sont toutes rationnelles entre elles, il est possible de trouver une période cyclique commune $T_C$ multiple de chacune des périodes cycliques $T_n$. Dès lors, l'ensemble des $\left\{\nu_i\right\}$ engendrera une fréquence commune $1/T_C$.

Afin d'illustrer le calcul de la période commune nous allons nous baser sur un exemple concret : les engrenages. La figure présente le multiplicateur utilisé au LIS^1.3 dans le cadre de l'Action Incitative Diagnostic et Signal^1.4. Le multiplicateur présenté sur la figure est constitué de roues ayant respectivement $n_1=57$ et $n_2=15$ dents.

Figure: Banc d'essais du LIS

Les deux roues tournent à des vitesses différentes, elles vont générer des signaux périodiques de périodes $\Theta_1=2\pi$ et $\Theta_2=2\pi\cdot \frac{n_2}{n_1}$. A chaque tour de la roue menante, il y a 57 contacts entre les dents des deux roues (la roue menante engrène la roue menée). Néanmoins, les dents en contact ne sont pas les mêmes d'un tour à l'autre. De plus, la surface de chaque dent n'est pas rigoureusement identique et particulièrement si il y a un défaut. Dès lors, le phénomène d'engrènement va introduire une période commune $\Theta_C$. Le terme $\Theta_C$ correspondra à l'angle nécessaire pour que l'engrenage revienne dans la même configuration (mêmes dents en contact).

La période commune correspond à un nombre de dents égal au plus petit commun multiple (ppcm) de $n_1$ et $n_2$. Soit :

$$\Theta_C=\Theta_1 \cdot \frac{ppcm\left(n_1,n_2\right)}{n_1}=\Theta_2 \cdot \frac{ppcm\left(n_1,n_2\right)}{n_2}$$ (1.36)

La figure présente des signaux issus de ce réducteur. Les bandes alternativement noires et blanches indiquent respectivement, la période de rotation de l'arbre d'entrée $\Theta_1$, la période de rotation de l'arbre de sortie $\Theta_2$, et, la période commune $\Theta_C$. En regardant attentivement les bandes, on vérifiera que l'on a une synchronisation des bandes tous les $\Theta_C$ degrés. Dans notre cas, la période commune correspond à $\lambda=5$ tours de l'arbre d'entrée et à $\beta=19$ tours de l'arbre de sortie. En regardant la figure nous apercevons nettement la période correspondant à l'arbre d'entrée qui module fortement le signal. Cette forte modulation est due au très mauvais état du réducteur et plus particulièrement de la roue menante. La période commune est difficile à déceler sur cette figure.

Figure: Signal polycyclostationnaire

Afin de mettre en évidence cette périodicité, le signal accélérométrique a été découpé en tranches correspondant à un cycle commun. Les tranches étant ensuite affichées les unes en dessous des autres (figure ). La période commune est multiple des périodes de rotation de l'arbre d'entrée et de l'arbre de sortie. Il est donc possible de considérer uniquement cette période comme le suggère la figure . Dans ce cas, le signal devient cyclostationnaire, et, est beaucoup plus simple à étudier, néanmoins, on ne prend plus en compte la contribution de chacune des roues.

Figure: Superposition de périodes communes

Nous allons donner un exemple qui va fortement nuancer cette approche, les signaux proviennent d'un réducteur fabriqué par la société FOC-MANQUAT utilisé au LASPI^1.5. La figure montre une roue du réducteur (à gauche), le réducteur (au milieu) ainsi que son schéma cinématique (à droite). Soit $n_i$ le nombre de dents correspondant à la $i^\text{\tiny ème}$ roue, tel que $i=1$ pour l'arbre d'entrée, et $I$ le nombre de roues. Pour notre réducteur, nous avons $\vect{n}=\left[23,62,15,70,18,59,18,61\right]$ et $I=8$.

Figure: Réducteur du LASPI

Pour ce type d'engrenage à plusieurs étages, il y a de nombreuses périodes de rotation: on pourra généraliser les développements précédents à chaque couple ou ensemble de roues pour calculer des périodes communes locales. Pour les engrenages à plusieurs étages, l'angle à partir duquel l'engrenage revient dans la même configuration va dépendre de toute la cinématique (nombre de dents). En généralisant l'équation , on obtient une période commune $\Theta_C$ :

$$\Theta_C=\Theta_1 \prod_{k=1}^{I/2} \frac{ppcm\left(n_{2k-1},n_{2k}\right)}{n_{2k-1}}$$ (1.37)

Afin d'illustrer cette formule, nous allons l'appliquer au réducteur du LASPI. Pour voir l'évolution de cette période en fonction du nombre d'étages du réducteur, nous allons la calculer pour les 2 premières roues, les 4 premières, ...

Nombre de paires de roues prises en compte	1	2	3	4
Période commune (tours)	62	868	51 212	3 123 932
Durée (1500 trs/min)	3 s	35 s	34 min	1,5 jour

Nous constatons alors que plus le nombre d'étages du réducteur devient grand, plus il est irréaliste de travailler sur certaines périodes communes très grandes. Pour réaliser des statistiques basées sur la période commune, il est nécessaire d'enregistrer un grand nombre de cycles. Une limite à $30$ cycles correspond à une durée d'acquisition de $1$ mois et $2$ semaines. Cette problématique nous amènera à définir plus loin la semicyclostationnarité et la pseudo-cyclostationnarité. Considérer qu'un signal d'engrenage polycyclostationnaire se réduit à un signal cyclostationnaire, ne fonctionne que pour des réducteurs ayant un faible nombre d'étages.

En pratique, on se focalisera sur les périodes cycliques que l'on souhaite étudier. Les périodes cycliques plus longues seront tronquées lors de l'acquisition ``trop courte''. Elles n'apparaîtront donc plus en tant que périodes mais comme un signal pseudo aléatoire. Il est donc important de ne pas perdre de vue que les résultats seront biaisés (voir chapitre pour plus de détails).

1.3.2.3 Périodes cycliques non rationnelles (ou quasi-cyclostationnarité)

Ce type de polycyclostationnarité est appelé quasi-cyclostationnarité par Gardner [#!gardner:stationarizable!#].

La quasicyclostationnarité intervient par exemple, dans le signal où il y a présence d'une composante d'origine électrique et d'une composante d'origine mécanique. La figure présente au centre un signal acquis par un ensemble capteur/conditionneur de mauvaise qualité. Le capteur de type vibratoire était pollué par le secteur à $50\;Hz$. Ce signal est donc quasicyclostationnaire. En se synchronisant sur la période cyclique mécanique, il a été possible, par moyennage synchrone de séparer la composante mécanique périodique de la composante électrique. Cet exemple montre que les signaux quasicyclostationnaires posent moins de problème que les signaux polycyclostationnaires pour l'estimation des différentes composantes, puisque les exponentielles de Fourier associées aux différentes fréquences fondamentales ainsi qu'à leurs harmoniques sont disjointes. Néanmoins, leur séparation devient délicate si les fréquences sont ``relativement proches'' (canaux non distincts sur une densité spectrale pour le pas d'échantillonnage utilisé).

C'est aussi le cas des signaux de machines asynchrones qui tournent à une fréquence légérement inférieure à la fréquence du champ tournant (phénomène de glissement). Ce champ tournant est lui même lié à la fréquence d'alimentation par un coefficient correspondant au nombre de paires de pôles. Dès lors, les fréquences associées aux signaux électriques et mécaniques sont situées à des fréquences très proches et sont alors difficiles à distinger.

Figure: Décomposition d'un signal quasicyclostationnaire

1.3.3 Semicyclostationnarité

Le concept de cyclostationnarité est essentiellement théorique. Il est impossible de vérifier expérimentalement la cyclostationnarité en raison même de la durée finie de toute expérience. On propose alors d'adapter le concept de semistationnarité tel qu'il est présenté dans [#!picinbono:signaux2!#] aux signaux cyclostationnaires.

Soit :

• un domaine $\mathcal{D}_y=\left[\theta_1,\theta_2\right]$,
• un signal réel cycloergodique et cyclostationnaire $x\left(\theta\right)$ de période cyclique $\Theta$, et,
• un autre signal réel $y\left(\theta\right)$ tel que :
  

  $$y\left(\theta\right)=\left\{ \begin{array}{ll} x\left(\th... ...~\mathcal{D}_y$} \\ 0 & \text{ailleurs} \end{array}\right.$$ (1.38)

  
  

Bien que $y\left(\theta\right)$ ne soit pas cyclostationnaire, car de durée finie, il vérifie cependant () ou () si $\theta$ et $\theta+\Theta$ sont dans $\mathcal{D}_y$. On dit alors que $y\left(\theta\right)$ est semicyclostationnaire si $\theta_2-\theta_1\gg\max\left(\Theta,\theta_c\right)$ où $\theta_c$ représente les constantes ``d'angles'' du système<sup>1.6</sup>. L'utilisation de $\Theta$ sera importante pour les machines tournant ``très lentement'' et, $\theta_c$ prédominera pour les machines ``rapides''.

La définition de la semistationnarité peut être retrouvée en enlevant le préfixe cyclo et en supprimant $\Theta$ au profit de la longueur de corrélation $t_c$. La longueur de corrélation est le temps à partir duquel on considère que la fonction de corrélation est nulle. Dans le contexte cyclostationnaire $t_c$ ne peut être défini puisque la fonction d'autocorrélation est périodique, c'est pourquoi nous le remplaçons par $\Theta$ et par $\theta_c$. Ainsi, nous reprenons l'idée qu'il est nécessaire de connaître le signal sur une durée supérieure aux constantes de temps du système afin de pouvoir tirer des conclusions pertinentes. Dans le cas des signaux cyclostationnaires la fonction de corrélation n'est pas décroissante mais périodique, on pourra alors estimer la période suivante à partir de la période précédente.

En général, lorsque l'on traite des signaux issus de l'expérimentation, on parle par abus de langage de cyclostationnarité et d'estimation au lieu de semicyclostationnarité. Considérer un signal semicyclostationnaire signifie tout simplement que l'on a acquis suffisamment de points pour l'analyser.

1.3.4 Pseudo-cyclostationnarité

L'hypothèse de semicyclostationnarité n'est pas toujours valide. Par exemple, si l'enregistrement est trop court pour observer l'ensemble des périodes cycliques, ou dans le cas de réducteurs à engrenage dont le rapport de réduction est important. Le processus bien que cyclostationnaire n'apparaît pas en tant que tel sur le signal.

Par ailleurs, un signal peut apparaître cyclostationnaire pour une observation, donnée alors qu'il est non stationnaire. Lors d'une observation certains paramètres apparaissent constants (niveau d'huile, état d'usure du système, ...). Après un certain temps (par exemple 500 000 km pour des roulements de roue d'automobile), on peut noter l'évolution de paramètres qui apparaissaient comme constants. D'autre part, certaines approximations ne seront plus valables (la fluctuation autour de la période moyenne sera de plus en plus importante dans un procédé de type marche aléatoire comme les roulements). On a donc ici une sorte de cyclostationnarité définie localement.

De tels signaux non semi-cyclostationnaires, seront appelés pseudo-cyclostationnaires.

1.3.5 Cyclostationnarité floue

Jusqu'à présent les définitions ont été données dans le domaine angulaire puisque la variable générique des machines tournantes est l'angle. Néanmoins, il est courant d'utiliser le temps pour échantillonner de tels signaux. Les signaux peuvent alors devenir non stationnaires et non cyclostationnaires à cause des fluctuations de vitesse. Il est néanmoins dommage dans ce cas de ne pas utiliser le fait que les signaux soient issus de machines cycliques. C'est pourquoi nous avons proposé de définir la cyclostationnarité floue afin de rétablir le lien avec la cyclostationnarité.

Nous désignerons sous le vocable ``cyclostationnaire floue'' les processus cycliques dont le ou les périodes cycliques sont variables qu'elles soient déterministes ou aléatoires.

Le chapitre sera consacré à l'étude de la cyclostationnarité floue.

1.4 Conclusion

Nous avons présenté dans ce chapitre les bases théoriques de la cyclostationnarité. La figure présente une synthèse des différents type de cyclostationnarité et leur lien avec la (non)-stationnarité sous forme de diagramme de Venn. La figure montre un organigramme permettant de déterminer facilement le type de cyclostationnarité.

Les chapitres suivant préciseront la notion de cyclostationnarité. Dans le chapitre nous allons présenter les différents types d'acquisitions (temporelle, angulaire), leurs avantages et inconvénients. Nous expliquerons également comment induire la cyclostationnarité pour les signaux temporels. Le chapitre montrera les aspects plus pratiques de la cyclostationnarité et rapportera des exemples dans le cas des signaux d'engrenages.

Ensuite nous ferons le lien entre la variable angulaire utilisée jusqu'à présent et la variable temporelle à l'aide de la cyclostationnarité floue. Cette dernière nous permettra également d'étudier les fluctuations de périodes cycliques. Le chapitre montrera comment exploiter des signaux de roulements produisant des signaux cyclostationnaires flous.

Figure: Différents types de cyclostationnarité et lien avec la (non)-stationnarité

Figure: Détermination du type de cyclostationnarité